Bonsoir
Je n'arrive pas à calculer cette intégrale :
f(x)=int(exp(-x^2*(1+t^2))/(1+t^2),t = 0 .. 1)
Et il faut en déduire int(exp(-x^2),t = 0 .. infinity)
Merci de votre aide
Olivier
Intégrale difficile à calculer
8 messages
- Page 1 sur 1
par amine801 » 10 Fév 2007, 21:26
Lintégrale nest pas calculable en utilisant les fonctions usuel(log exp
.ect) il faut utilise la fonction d'erreur de gauss
petit lien si tu connaît pas http://fr.wikipedia.org/wiki/Fonction_d'erreur
petit lien si tu connaît pas http://fr.wikipedia.org/wiki/Fonction_d'erreur
par alex26 » 10 Fév 2007, 22:06
Je pense que c calculable car c tombé à un oral de concours. C'est probablement pour ca qu'il y a les 1+t²
par abcd22 » 10 Fév 2007, 22:30
Bonsoir,
Essaie de calculer f´(x) (dérivation sous le signe intégrale...) puis f en primitivant (f(0) est facile à calculer).
Essaie de calculer f´(x) (dérivation sous le signe intégrale...) puis f en primitivant (f(0) est facile à calculer).
par fahr451 » 10 Fév 2007, 23:19
bonsoir
je n'arrive pas directement comme abcd semblait le dire
j'ai quelques calculs (que je nai pas vérifiés)
1) intégration par parties
intégrer 1 dériver le reste
f(x) = exp(-2x^2) /2 +2(1+x^2) intégrale t^2 /(1+t^2)^2 exp ( ) dt
2)en posant F(x) = intégrale exp ( ) /(1+t^2)^2 dt
la dérivation sous le signe intégrale pour F donne
F'(x) = -2x f(x)
3) équa diff en F du premier ordre linéaire avec second membre
la résolution se fait bien; la variation de la constante donnant explicitement
une sol particulière
4) à toi de finir.
je n'arrive pas directement comme abcd semblait le dire
j'ai quelques calculs (que je nai pas vérifiés)
1) intégration par parties
intégrer 1 dériver le reste
f(x) = exp(-2x^2) /2 +2(1+x^2) intégrale t^2 /(1+t^2)^2 exp ( ) dt
2)en posant F(x) = intégrale exp ( ) /(1+t^2)^2 dt
la dérivation sous le signe intégrale pour F donne
F'(x) = -2x f(x)
3) équa diff en F du premier ordre linéaire avec second membre
la résolution se fait bien; la variation de la constante donnant explicitement
une sol particulière
4) à toi de finir.
par Joker62 » 11 Fév 2007, 00:52
Salut tous 
Donc en fait, le problème c'est de pouvoir calculer
Pour celà on insère la fonction = \int_0^{+\infty} \frac {e^{-x^2(u^2+1)}}{u^2+1}du)
On voit immédiatement que cette intégrale converge.
Et on insère = \int_0^n \frac {e^{-x^2(u^2+1)}}{u^2+1}du)
De plus = \frac {e^{-x^2(u^2+1)}}{u^2+1})
et donc = \int_0^n f(x,u) du)
f est clairement continue sur
donc sur 
Donc 
est continue sur 
De plus_{n \ ge 1})
converge uniformément vers F ce qui prouve que F est continue.
On dérive F par rapport à x :
})
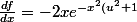qui est continue sur d'où les sont continûment dérivable sur et :
 = -2x \int_0^n e^{-x^2(u^2+1)}du)
Il faut vérifier que_{n \ge 1})
converge uniformément pour tout compact de 
on utilise le fait qu'elle est uniformément de Cauchy.
On a alors : = lim_{n\rightarrow +\infty} F'_n(x) = -2xe^{-x^2}\int_0^{+\infty} e^{-x^2u^2}du)
On pose v = xu et on retrouve l'intégrale de Gauss
 = -2xe^{-x^2} \int_0^{+\infty} e^{-v^2}dv)
Tu as = -2Ie^{-x^2})
F' continue, ça implique d'après le théorème fondamental du calcul intégrale :
-F(A) = -2I \int_A^B e^{-x^2}dx)
On fait tendre A vers 0, B vers +oo
F continue ça implique que = F(0))
Avec = \frac {\pi}{2})
F(B) tend clairement vers 0 quand B tend vers +oo
D'où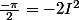
et donc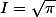 
Rendons à Caesar ce qui est à Caesar, Merci à mon prof d'ANA3
Mr Lee
Donc en fait, le problème c'est de pouvoir calculer
Pour celà on insère la fonction
On voit immédiatement que cette intégrale converge.
Et on insère
De plus
et donc
f est clairement continue sur
De plus
On dérive F par rapport à x :
Il faut vérifier que
On a alors :
On pose v = xu et on retrouve l'intégrale de Gauss
Tu as
F' continue, ça implique d'après le théorème fondamental du calcul intégrale :
On fait tendre A vers 0, B vers +oo
F continue ça implique que
Avec
F(B) tend clairement vers 0 quand B tend vers +oo
D'où
Rendons à Caesar ce qui est à Caesar, Merci à mon prof d'ANA3
Mr Lee par fahr451 » 11 Fév 2007, 08:34
bonjour je ne suis pas d'accord avec joker les bornes étaient 0 et 1 et non 0 +infini dans le problème posé
car si le but est de calculer l'intégrale de la gaussienne un coup d 'intégrale double et le tour est joué.
car si le but est de calculer l'intégrale de la gaussienne un coup d 'intégrale double et le tour est joué.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :