[1°S] : Les suites géométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 19:22
par Pekwylechti » 05 Fév 2007, 19:22
Bonsoir à tous et merci de prêter attention à ma discussion....
J'ai du mal à résoudre certaines questions à propos du problème suivant...
On considère la suite (Un) n appartenant à IN* définie par :

Partie 1 :
- Démontrer que cette suite est majorée par 3 [résolu]
- Démontrer que cette suite est monotone [résolu]
- Démontrer que cette suite est convergente. Calculer sa limite l [résolu]
Partie 2 :
On considère la suite (Vn) n appartenant à IN* définie pour tout entier naturel n non nul par : Vn = n(3-Un)
- Démontrer que cette suite est une suite géométrique dont on précisera le premier terme et la raison. [non résolu]
- Exprimer Vn puis Un en fonction de n. Retrouver la lamite de la suite (Un) n appartenant à IN* [non résolu]
Quelqu'un pourrait me secourir ?
D'avance merci...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 19:42
par sue » 05 Fév 2007, 19:42
bonsoir,
(3-U_{n+1})}{n(3-U_n)} = \frac{(n+1)(3-\frac{nu_n}{2(n+1)}-\frac{3(n+2)}{2(n+1)})}{n(3-u_n)} = \frac{6(n+1)-3(n+2)-nu_n}{2n(3-u_n)} =...)
ben tu peux continuer, tu trouvera qq chose à simplifier.. :we:
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 20:03
par Pekwylechti » 05 Fév 2007, 20:03
sue a écrit: (3-U_{n+1})}{n(3-U_n)} = \frac{(n+1)(3-\frac{nu_n}{2(n+1)}-\frac{3(n+2)}{2(n+1)})}{n(3-u_n)} = \frac{6(n+1)-3(n+2)-nu_n}{2n(3-u_n)} =...)
Merci,
= 6(n+1)-3(n+1)-3(n+2)-nUn
.._______________________ = ....... ??? Je comprends pas quoi faire ensuite ?
............2n (3-Un)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 20:06
par sue » 05 Fév 2007, 20:06
tu dévellope le numérateur puis tu simplifie...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 20:09
par sue » 05 Fév 2007, 20:09
Pekwylechti a écrit:
= 6(n+1) -3(n+1) -3(n+2)-nUn
.._______________________ = ....... ???
............2n (3-Un)
y a pas de -3(n+1) ...
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 20:30
par Pekwylechti » 05 Fév 2007, 20:30
Ce qui donne :
6n+6-3n-6-nUn = 3n - nUn ?
Et ensuite je dois procéder comment ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 20:40
par sue » 05 Fév 2007, 20:40
donc tu as
} = \frac{n(3-u_n)}{2n(3-u_n)} = ...)
tu simplifie par ..., tu détermine ainsi la raison de
)
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 20:52
par Pekwylechti » 05 Fév 2007, 20:52
Ce qui donne :
n/2n soit 1/2
donc q = 1/2 ? C'est bien cela ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 21:04
par sue » 05 Fév 2007, 21:04
oui c'est bien :we:
bon aprés pour déterminer

en fonction de n , il faut d'abord déterminer

en fonction de n .
tu sais que

donc
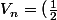^nV_1)
, tu calcule
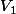
.
aprés on a
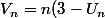)
donc

ensuite tu remplace

par sa forme en fonction de n déjà déterminée .
ok ?
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 21:12
par Pekwylechti » 05 Fév 2007, 21:12
V1 = 2
dc Vn =
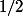

x2
= n
Jusque là c'est bon ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 21:24
par sue » 05 Fév 2007, 21:24
ah non attention !
^n = 2\times \frac{1}{2^n} = 2\times \frac{1}{2\times 2^{n-1}} = \frac{1}{2^{n-1}}= (\frac{1}{2})^{n-1})
sinon tu peux garder juste
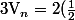^n)
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 21:27
par Pekwylechti » 05 Fév 2007, 21:27
D'accord ! et pour Un ça marche comment alors ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 21:30
par sue » 05 Fév 2007, 21:30
relis ce que j'ai dis précédemment à propos !
-
Pekwylechti
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Déc 2005, 19:20
-
 par Pekwylechti » 05 Fév 2007, 21:38
par Pekwylechti » 05 Fév 2007, 21:38
sue a écrit:oui c'est bien :we:
bon aprés pour déterminer

en fonction de n , il faut d'abord déterminer

en fonction de n .
tu sais que

donc
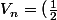^nV_1)
, tu calcule
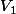
.
aprés on a
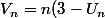)
donc

ensuite tu remplace

par sa forme en fonction de n déjà déterminée .
ok ?
Donc
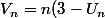)
donc

je remplace Vn par 2(1/2)^n et je simplifie ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 05 Fév 2007, 21:44
par sue » 05 Fév 2007, 21:44
tu n'as rien à simplifier :
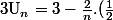^n)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités

