Primitive et intégration!

par **el juli** » 31 Jan 2007, 16:23

Bonjour bonjour!!!

Alors pour mon premier post voici un petit calcul d'intégrale^^

f(x)=(x-1)(e^x²-2x) et intégrale définie sur [1;2]

J'ai ecayer la résolution de mon intégrale en apliquant le raisonement par partie mais je suis allégrement bloqué..

Help!!je cherche surtout une démonstration et non pas un résultat!

Merci et bonne journée :++:

par **anima** » 31 Jan 2007, 16:27

el juli a écrit:Bonjour bonjour!!!

Alors pour mon premier post voici un petit calcul d'intégrale^^

F(x)=(x-1)(e^x²-x) et intégrale définie sur [1;2]

J'ai ecayer la résolution de mon intégrale en apliquant le raisonement par partie mais je suis allégrement bloqué..

Help!!je cherche surtout une démonstration et non pas un résultat!

Merci et bonne journée :++:

Je ne pense pas que tu puisse l'intégrer au niveau du lycée. Les primitives de e^x² ne sont pas exprimables grâce aux fonctions usuelles, donc... Relis ton texte, si c'est nommé F(x), c'est que c'est déjà une primitive :mur:

par **el juli** » 31 Jan 2007, 16:31

Salut et quelle rapiditée^^

Alors Alors rectification....f(x) et non pas F(x), le syndrome de la touche maj en début de phrase....

Et confirmation f(x)=(x-1)(e^x²-2x) (Livre : collection RADIAL maths terminales S)

Merci!

par **fonfon** » 31 Jan 2007, 17:14

Salut,

c'est bien cette integrale qu'il faut calculer?

ça va être dur d'integrer

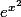
en terminale

il n'y a pas d'autres question avant?

par **Nightmare** » 31 Jan 2007, 17:16

Bonjour

Ce n'est pas parce que l'on appelle F une fonction que c'est une primitive, ça n'a aucun sens...

par **anima** » 31 Jan 2007, 17:17

Nightmare a écrit:Bonjour

Ce n'est pas parce que l'on appelle F une fonction que c'est une primitive, ça n'a aucun sens...

C'était une SUPPOSITION, Nightmare. Parce que sinon, intégrer e^x² en terminale est tout aussi impossible...

par **el juli** » 31 Jan 2007, 17:35

Voila exactment pour "fonfon" a noter que le "-2x" est associer à l'exponentielle!

Simpas mon exo nan?^^

Sachant également que je vient de voir les intégrations par partie, mais pourtant ca me donne un truk horrible.... :mur:

par **fonfon** » 31 Jan 2007, 17:52

ça change tout il faut penser à bien mettre les parenthéses

une idée

tu transformes un peu

et oui il faut faire IPP maintenant

par **Nightmare** » 31 Jan 2007, 18:40

(x²-2x)'=2x-2=2(x-1)

On en déduit directement que l'intégrale vaut

:happy3:

par **el juli** » 31 Jan 2007, 19:21

hum....

oki oki!!!!! pas fole la guepe^^
Je fais ca des ce soir j'ecaye par particion des que je finit ma philo :hum:

Merci mille fois!

Primitive et intégration!

Primitive et intégration!

Qui est en ligne