Problème avec un exercice
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
boulette06
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Jan 2007, 15:36
-
 par boulette06 » 30 Jan 2007, 16:12
par boulette06 » 30 Jan 2007, 16:12
rebonjour!
dsl de vous déranger mais j'ai encore un autre soucis et plus grave car je men sors vraiment pas. si vous pouviez au moins m'expliquez la première question ce serait vraiment gentl merci.
Dans un repere (o,i,j) on donne les points A(0;2),B(3;5) et Gm(m;m²) où m est un nombre réel.
1) Pour quelles valeurs de m, le point Gm peut être considéré comme barycentre de A et de B ?
2) Pour chacune des valeurs de m trouvées précédemment, déterminer les coefficients a et b tels que Gm soit le barycentre des points pondérés (A;a) et (B;b).
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Jan 2007, 16:15
par annick » 30 Jan 2007, 16:15
Bonjour,
il faut donc que tu trouves les valeurs pour lesquelles GA+GB=0
Tu calcules les coordonnées de GA et GB et tu cherches pour quelles valeurs de m la somme de ces coordonnées sont nulles
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Jan 2007, 16:32
par annick » 30 Jan 2007, 16:32
je crois finalement qu'il y a une meilleure méthode :
si G barycentre de A,B, cela veut dire que GA colinéaire à AB
Soit GA=kAB
Tu calcules donc les coordonnées de GA et AB et tu trouves 2 relations contenant k.
Tu les égalises et tu trouves une équation du 2ème degré en m² que tu résouds
-
boulette06
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Jan 2007, 15:36
-
 par boulette06 » 30 Jan 2007, 16:33
par boulette06 » 30 Jan 2007, 16:33
en faisant xce que tu m'as dit j'ai calculé les coordonnées des vecteurs puis j'ai utilisé la propriété de la colinéarité des vecteurs qui est xy'-yx'=0 ce qui ma donné -3m + 2m au cube -3m²-6=0 mais j'ai 'impression que je me suis trompé quelque part parce qu'il y a des cubes...
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 30 Jan 2007, 16:34
par rene38 » 30 Jan 2007, 16:34
Bonjour
boulette06 a écrit:1) Pour quelles valeurs de m, le point Gm peut être considéré comme barycentre de A et de B ?
Gm est barycentre de A et B ssi Gm est un point de la droite (AB) autre que A et B.
ça sent les vecteurs colinéaires ... par exemple

-
lexot
- Membre Relatif
- Messages: 179
- Enregistré le: 25 Déc 2006, 06:16
-
 par lexot » 30 Jan 2007, 16:36
par lexot » 30 Jan 2007, 16:36
Bonjour
Pour que Gm soit le barycentre des points A et B, il faut que

et

soient colinéaires, car
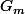
se trouve sur la droite (AB) :
Après la résolution de l'équation en m, on trouve S = {-1;2}
Cordialement
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Jan 2007, 16:38
par annick » 30 Jan 2007, 16:38
GA(-m,(2-m²)), AB(3,3)
Donc
-3m-3(2-m²)=0
-m-2+m²=0
m²-m-2=0
Il faut maintenant résoudre cette équation
-
boulette06
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Jan 2007, 15:36
-
 par boulette06 » 30 Jan 2007, 16:39
par boulette06 » 30 Jan 2007, 16:39
a mais oui bien sur! c'est moi qui me suis trompé de vecteur! merci de votre aide j'éspère qu'en faisnt mon calcul je vais trouvé ca.
-
boulette06
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Jan 2007, 15:36
-
 par boulette06 » 30 Jan 2007, 16:57
par boulette06 » 30 Jan 2007, 16:57
Juste pr savoir pour la dernière question il existe couples de barycentre c'est bien ca?
-
boulette06
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Jan 2007, 15:36
-
 par boulette06 » 30 Jan 2007, 16:58
par boulette06 » 30 Jan 2007, 16:58
enfin je voulais dire 4 couples
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Jan 2007, 17:32
par annick » 30 Jan 2007, 17:32
non, cela ne fait pas 4 couples, mais 2 couples (a,b): un pour G(-1) et un pour G2 correspondant à m=-1 et m=2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités

