Oups ! Je suis désolé de me montrer insistant...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 21 Jan 2007, 18:59
par r21883 » 21 Jan 2007, 18:59
Bonsoir,

Taux de variation :
 - f(a)}{b-a})

On utilise la formule On utilise la formule
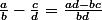
(a-1) - (2a+)(b-1)}{(b-1)(a-1)}}{b-a}=)
On utilise la formule
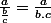
(a-1) - (2a+)(b-1)}{(b-a)[(b-1)(a-1)]}=)
On développe le numérateur et on le simplifie
(b-1)(a-1)}=)
(b-1)(a-1)}=)
}{(b-a)(b-1)(a-1)}=)
}{- (b-a)(b-1)(a-1)}=)
}{(b-a)(-b+1)(a-1)}=)
(a-1)}=)
Maintenant que l'on a calculé le taux de variation de

entre les valeurs a et b
c.-à-d.
(-b+1)}})
(sur le précedent fil, j'avais fait une erreur qui est maintenant rectifié :we: enfin j'espère)
La question 2 est :
En utilisant le taux de variation prouver que

est strictement croissante sur

et

Et je ne sais pas comment faire, merci de votre aide pour me préciser la démarche
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 21 Jan 2007, 19:33
par r21883 » 21 Jan 2007, 19:33
Up SVP et merci de votre aide.
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 21 Jan 2007, 20:27
par r21883 » 21 Jan 2007, 20:27
Plus personne à cette heure pour un coup de main ?
Merci
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 21 Jan 2007, 23:01
par r21883 » 21 Jan 2007, 23:01
SVP ? Merci
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 22 Jan 2007, 21:43
par r21883 » 22 Jan 2007, 21:43
J'essaye une nouvelle fois de faire remonter :help:
Merci
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 22 Jan 2007, 21:46
par Clembou » 22 Jan 2007, 21:46
r21883 a écrit:Bonsoir,

Taux de variation :
 - f(a)}{b-a})

On utilise la formule On utilise la formule
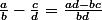
(a-1) - (2a+)(b-1)}{(b-1)(a-1)}}{b-a}=)
On utilise la formule
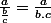
(a-1) - (2a+)(b-1)}{(b-a)[(b-1)(a-1)]}=)
On développe le numérateur et on le simplifie
(b-1)(a-1)}=)
(b-1)(a-1)}=)
}{(b-a)(b-1)(a-1)}=)
}{- (b-a)(b-1)(a-1)}=)
}{(b-a)(-b+1)(a-1)}=)
(a-1)}=)
Maintenant que l'on a calculé le taux de variation de

entre les valeurs a et b
c.-à-d.
(-b+1)}})
(sur le précedent fil, j'avais fait une erreur qui est maintenant rectifié :we: enfin j'espère)
La question 2 est :
En utilisant le taux de variation prouver que

est strictement croissante sur

et

Et je ne sais pas comment faire, merci de votre aide pour me préciser la démarche
On doit faire quoi ? Corriger la question 1 ? Faire la deuxième question ? :we:
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 22 Jan 2007, 23:40
par r21883 » 22 Jan 2007, 23:40
Bonsoir Clembou,
A vos questions, les réponses dans l'ordre sont :
- Me conseiller sur la démarche pour la résolution de la question 2
- Oui si les calculs sont erronés
- Ne pas faire la 2ième question mais se reporter à ma première réponse :)
Merci,
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 24 Jan 2007, 20:57
par r21883 » 24 Jan 2007, 20:57
Bonsoir,
Up SVP :)
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 24 Jan 2007, 21:52
par annick » 24 Jan 2007, 21:52
Tout d'abord tes calculs sont entièrement justes.
Ensuite, on considère a et b très proches de x, donc x sensiblement égal à a et b
Ton taux de variation devient t=3/(1-x)(x-1)=-3/(x-1)² Ce taux est toujours négatif car (x-1)² toujours positif, donc ta fonction est toujours décroissante, ce que tu peux facilement vérifier sur ta calculatrice
Bon courage pour finir
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 25 Jan 2007, 23:02
par r21883 » 25 Jan 2007, 23:02
Merci Annick de ta réponse, comme quoi il faut parfois se montrer légerement 'insistant" :we:
Au sujet de ta réponse, n'y a t-il rien de plus "formel" comme démonstration que de dire "on considère a et b très proches de x, donc x sensiblement égal à a et b..."
Encore merci bcp :++:
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 26 Jan 2007, 19:41
par r21883 » 26 Jan 2007, 19:41
Bonsoir,
...mais j'ai une interrogation lundi 29/01 et ne sais toujours pas comment en partant dun taux de variation je peux prouver quune fonction est strictement croissante (ou décroissante, voir pas strictement) sur des intervalles donnés.
Merci de vos conseils et/ou lien(s) sur des cours qui me permettront de comprendre / appréhender la démarche.
Encore merci de votre aide sur le sujet.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 26 Jan 2007, 20:08
par abcd22 » 26 Jan 2007, 20:08
Bonsoir.
Par définition, f est strictement croissante sur l'intervalle I si pour tous a, b dans I tels que a 0[/TEX] (si b>a le numérateur et le dénominateur sont positifs, si b 0[/TEX], puis pareil si a > 1 et b > 1.
En fait le taux de variation entre a et b est le coefficient directeur de la droite qui relie les points d'abscisses a et b de la courbe représentative de f : s'il est positif, la droite « monte », si la droite monte pour tous les couples de points de l'intervalle ça veut dire que f est croissante.
Pour f croissante pas forcément strictement le taux de variation doit être positif ou nul, pour décroissante et strictement décroissante on remplace « positif » par « négatif ».
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 26 Jan 2007, 20:12
par annick » 26 Jan 2007, 20:12
Si ton taux de variation est positif cela veut dire que ta fonction croît. En effet, cela veut dire que si x croît, y croît aussi (essaye des prendre un exemple en traçant n'importe quel type de courbe croissante ou décroissante)
De même si ton taux de variation est négatif, alors f décroît.
-
r21883
- Membre Naturel
- Messages: 42
- Enregistré le: 20 Jan 2007, 12:37
-
 par r21883 » 28 Jan 2007, 11:52
par r21883 » 28 Jan 2007, 11:52
Merci beaucoup à vous deux annick et abcd22 :++:
Et aussi aux autres qui tout comme vous, prenez sur votre temps libre pour nous aider.
Encore, un grand merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités
