Plan dans l'espace

[mathis]

Bonjour,

Comment ferriez vous pour donner l'equation du plan P , sachant que les point A(-1;2;1) , B(1;-6;-1) et C(2;2;2) appartiennent au plan ...


merci d'avance

[anima]

Bonjour,

Comment ferriez vous pour donner l'equation du plan P , sachant que les point A(-1;2;1) , B(1;-6;-1) et C(2;2;2) appartiennent au plan ...


merci d'avance

Trouve les vecteurs AB et AC, et fais en le produit vectoriel pour trouver le vecteur normal

[lexot]

Bonjour

Le produit vectoriel n'est pas au programme de TS. Cherche un vecteur n normal au plan ABC (vecteurs AB et AC). Ce vecteur n sera normal au vecteur AM M(x;y) du plan ABC, et tu trouveras l'équation du plan : ax+by+cz+d=0

Cordialement

[anima]

Bonjour

Le produit vectoriel n'est pas au programme de TS. Cherche un vecteur n normal au plan ABC (vecteurs AB et AC). Ce vecteur n sera normal au vecteur AM M(x;y) du plan ABC, et tu trouveras l'équation du plan : ax+by+cz+d=0

Cordialement

HEIN?

Tu rigoles là, j'espère. Donc ils ont de la géométrie "abrégée", dans les lycées en France? Pas croyable. Quand je pense qu'un tiers de mon prébac ici (école européenne) portait sur des applics du produit vectoriel...Ca fait peur :doh:

[lexot]

Bonjour

(2;-8;-2) ; (3;0;1)
(1;1;-3) ; (x+1;y-2;z-1)

En faisant le produit scalaire . = 0, on a l'équation du plan :
x+y-3z+2=0

Cordialement

[fahr451]

bonjour

lexot quelle est la méthode proposée pour trouver un vecteur orthogonal à AB et AC ?

[lexot]

Bonjour

Pour trouver le vecteur orthogonal (x';y';z') avec un autre vecteur 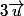(x;y;z), il faut que x.x'+y.y'+z.z'=0. Voici ce que je propose : quand un vecteur a une coodonnée nulle, et c'est le cas de , on commence par lui.

Je prends x'=1 (valeur la plus évidente, mais on peut changer), donc z'=-3, car (1).(3)+(-3).(1)=0
donc .=0
En faisant .=0, on trouve y'=1

Cette méthode a l'avantage d'être rapide!!!
Sinon, une méthode classique consisterait à poser x'=1, et d'écrire un système de 2 équations à 2 inconnues avec y' et z'.

2 -8y' -2z' = 0
3 +0y' +z' = 0
on retrouve (1;1;-3)

Cordialement

[fahr451]

merci bien

le produit vectoriel était il si compliqué qu'il fallait le retirer des programmes?

[lexot]

Bonjour

Je réponds à la question de fahr451.
Résolution de l'équation : - 4x + 3 = 0

En 2nde : - = 0
ou (x-1)(x-3)=0 ; et S={1;3}

En 1ère on utilise delta= -4ac

Je pense qu'un élève de 2nde est capable d'utiliser les outilis de 1ère, mais on l'entraine à manipuler des expressions avant de lui fournir des outils plus puissants. Donc, c'est une question de choix de programme, fait à un niveau ministériel. De même un élève de Tle est capable d'utiliser le produit vectoriel.

Cordialement