Esperance
40 messages
- Page 1 sur 2 - 1, 2
Esperance
Bonjur,
J'ai deux variables aleatoires discretes X et Y dont je connais la loi conjointe, ainsi que les lois marginales (les va ne sont pas independantes).
Comment calculer l'esperance du coupe (X,Y) ?
Merci d'avance
J'ai deux variables aleatoires discretes X et Y dont je connais la loi conjointe, ainsi que les lois marginales (les va ne sont pas independantes).
Comment calculer l'esperance du coupe (X,Y) ?
Merci d'avance
Bonsoir,
En cherchant sur le net, j'ai vu quelque chose qui pourrait ressembler à ce que tu veux : l'espérance serait alors deux vecteurs (un pour chacune des variables)
pour X, c'est le vecteur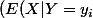)_{i}) dont la dim est celle des valeurs possibles de Y
dont la dim est celle des valeurs possibles de Y
et idem pour Y.
Bien entendu, ça n'a pas de sens pour des variables continues ?
En cherchant sur le net, j'ai vu quelque chose qui pourrait ressembler à ce que tu veux : l'espérance serait alors deux vecteurs (un pour chacune des variables)
pour X, c'est le vecteur
et idem pour Y.
Bien entendu, ça n'a pas de sens pour des variables continues ?
un petit exo récréatif sur l 'espérance conditionnelle (en discrét)
un explorateur se trouve dans le noir dans un réseau de galleries :
il peut prendre au hasard l'un des trois chemins A,B,C:
A le mène à la sortie en 5 heures
B le ramène au point de départ en 3 heures
C le ramène au point de départ en7heures
une fois ramené au point de départ il n'a aucun moyen de savoir lequel des trois chemins il a emprunté
quelle est la durée moyenne de son séjour sous terre?
un explorateur se trouve dans le noir dans un réseau de galleries :
il peut prendre au hasard l'un des trois chemins A,B,C:
A le mène à la sortie en 5 heures
B le ramène au point de départ en 3 heures
C le ramène au point de départ en7heures
une fois ramené au point de départ il n'a aucun moyen de savoir lequel des trois chemins il a emprunté
quelle est la durée moyenne de son séjour sous terre?
l'esperance d'un vecteur ou d'un couple (X,Y) ( ca veut dire la memem chose) , que les variables X et Y soit independantes ou pas est le vecteur (E(X),E(Y)).
Il faut donc que tu calcules l'esperance de X et l'esperance de Y.
Pour ca tu vas te servir de la loi jointe.
E(X)= Somme_sur_k (kP(X=k))
Or P(X=k)=somme_sur_i P(X=k,Y=i)
donc E(X)= Somme_sur_k (k somme_sur_i P(X=k,Y=i) )
Tu fais pareille pour Y.
et tu as ton esperance E((X,Y)) = (E(X),E(Y))
*Edit je viens de voir que en plus on te donnait les lois marginales, tu peux donc directement faire:
E(X)= Somme_sur_k (kP(X=k))
Meme pas besoin de la loi jointe.
Et tu fais pareille avec la loi de Y pour trouver E(Y)
Ensuite le resultat est:
E((X,Y))=(E(X),E(Y))
Il faut donc que tu calcules l'esperance de X et l'esperance de Y.
Pour ca tu vas te servir de la loi jointe.
E(X)= Somme_sur_k (kP(X=k))
Or P(X=k)=somme_sur_i P(X=k,Y=i)
donc E(X)= Somme_sur_k (k somme_sur_i P(X=k,Y=i) )
Tu fais pareille pour Y.
et tu as ton esperance E((X,Y)) = (E(X),E(Y))
*Edit je viens de voir que en plus on te donnait les lois marginales, tu peux donc directement faire:
E(X)= Somme_sur_k (kP(X=k))
Meme pas besoin de la loi jointe.
Et tu fais pareille avec la loi de Y pour trouver E(Y)
Ensuite le resultat est:
E((X,Y))=(E(X),E(Y))
Je precise que l'esperance conditionnelle n'a rien a voir ici.
Si on nous demandait l'esperance conditionnelle de X/Y par exemple:
cela serait G(y)=E(X|Y=y)= somme_sur_k (kP(X=k|Y=y))
G(y)=E(X|Y=y)=somme_sur_k (kP(X=k,Y=y)/P(Y=y)*)
*et dans le cas d'un probleme sans les lois marginales on remplacerait P(Y=y) par somme_sur_i (P(X=i,Y=y))
Mais ce n'est pas ce qu'on nous demande.
Si on nous demandait l'esperance conditionnelle de X/Y par exemple:
cela serait G(y)=E(X|Y=y)= somme_sur_k (kP(X=k|Y=y))
G(y)=E(X|Y=y)=somme_sur_k (kP(X=k,Y=y)/P(Y=y)*)
*et dans le cas d'un probleme sans les lois marginales on remplacerait P(Y=y) par somme_sur_i (P(X=i,Y=y))
Mais ce n'est pas ce qu'on nous demande.
40 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
