Facile

par **MikO** » 25 Déc 2006, 11:35

salut, ce n'est pas de niveau olympiade, mais ce qui minteresse est de voir comment vous allez vous y prendre pour resoudre cette inegalité.

soit a,b,c tq

et c>0

par **Patastronch** » 25 Déc 2006, 11:59

MikO a écrit:salut, ce n'est pas de niveau olympiade, mais ce qui minteresse est de voir comment vous allez vous y prendre pour resoudre cette inegalité.

soit a,b,c tq et c<0

Alors :

et

l'inégalité est donc impossible.

par **MikO** » 25 Déc 2006, 17:08

jai corrigé, cetait bien sur c>0 !

par **darkmaster** » 25 Déc 2006, 17:33

MikO a écrit:salut, ce n'est pas de niveau olympiade, mais ce qui minteresse est de voir comment vous allez vous y prendre pour resoudre cette inegalité.

soit a,b,c tq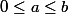 et c>0

Salut,

Il reste à montrer que

ou bien

( qui est vraie car

) et c'est bon.

par **MikO** » 25 Déc 2006, 18:43

javais fais ca autrement mais ta solution est bien plus rapide :)

par **sandrine_guillerme** » 23 Jan 2007, 17:56

Donne nous ta solution miko :p

par **MikO** » 23 Jan 2007, 20:21

mdr ?
Va= racine de a la flemme de passer en latex
soit le polynome, parametré par a,b tq 0 inferieur a inferieur b, c^2-c(Vb-Va)+b-a, tu calcule le discrimnant qui est tjs positif dans les conditions fixes =>
c^2-c(Vb-Va)+(b-a) superieur a 0 => c^2+b-a superieur c(Vb-Va)
comme c>0 => c+(b-a)/c superieur Vb-Va

une seule chose a dire tes vraimen trop conne, tu crois tjs ke jnai pa la solution du defi ke jai proposé ? mdr c seulemen ke jai la flem de copier en latex, dsl davoir une vie sociale ( pardon vraiment ! )

par **Imod** » 26 Jan 2007, 00:07

MikO a écrit:mdr ?
Va= racine de a la flemme de passer en latex
soit le polynome, parametré par a,b tq 0 inferieur a inferieur b, c^2-c(Vb-Va)+b-a, tu calcule le discrimnant qui est tjs positif dans les conditions fixes =>
c^2-c(Vb-Va)+(b-a) superieur a 0 => c^2+b-a superieur c(Vb-Va)
comme c>0 => c+(b-a)/c superieur Vb-Va

une seule chose a dire tes vraimen trop conne, tu crois tjs ke jnai pa la solution du defi ke jai proposé ? mdr c seulemen ke jai la flem de copier en latex, dsl davoir une vie sociale ( pardon vraiment ! )

Une telle insolence et une telle vulgarité pourrait être acceptée par quelqu'un qui a montré quelques traits de génie , pour le moment je n'ai vu que de la paresse , de l'arrogance et des solutions bêtement scolaires .

Imod

PS : Latex n'est pas si compliqué et l'utiliser est une marque de politesse envers ceux qui te lisent .

par **Dominique Lefebvre** » 26 Jan 2007, 16:57

Imod a écrit:Une telle insolence et une telle vulgarité pourrait être acceptée par quelqu'un qui a montré quelques traits de génie

Au delà de l'insolence, je détecte chez cet individu une certaine aigreur (aigritude ?) pathologique! Peut être est-ce du à une perception aigüe de la réalité de son état ....

Facile

facile

Qui est en ligne