Résolution d'une equation

[simonsays]

Bonjour à tous,
Mon problème est que je doit résoudre cette équation :

f(n)=3*f(n/4)+n, ou n est un entier positif.

Je n'ai pas d'idée sur comment proceder, donc si vous êtes en mesure de m'aider...

[chulzi]

c'est un peu flou!!!!

[simonsays]

Je comprend pas ce que tu trouves flou, ma question me paraît parfaitement claire.
(je cherche à déteminer la fonction f biensur si c'était ça que tu ne comprenais pas)

[tize]

J'ai pas cherché dans le détail, mais tu peux commencer par des fonctions simples du genre linéaire ou constante, il me semble que convient reste à savoir si c'est la seule...

[chulzi]

ok ok ok!!!! tu a f(0) =0.. c'est déja un début. donc ya pas de constante. a toi la suite.

[tize]

Un truc qui marche avec f continue...
Si f et g vérifient ta condition alors h(n)=f(n)-g(n) vérifie :

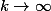
h étant continue, quand donc nécessairement sinon h(n) n'est pas définie et du coup donc f = g est une solution unique....

[simonsays]

merci beaucoup tize, d'avoir pris le temps de réfléchir pour me répondre.
Le probleme est qu ensuite je doit trouver la fonction f telle que :

f(n)=3f(n/4)+racine(n);

et là je ne suis pas sûr qu une simple fonction linéaire suffice.

Il y aurait il un raisonnement plus général pour résoudre ce type d'équations, avec une équation caractéristique par exemple, comme pour résoudre une equa diff ou bien un suite récurente...?

[fahr451]

tize pourquoi du coup h(n) = 0 ? si h dérivable en 0 oui je suis d 'accord sinon ?

pour le deuxième exemple

f0(x) = -2racine (x) convient

pour l'unicité
malheureusement on ne peut supposer f dérivable puisque la solution particulière ne l 'est pas .

[tize]

tize pourquoi du coup h(n) = 0 ? si h dérivable en 0 oui je suis d 'accord sinon ?...

Oui tu as raison, je me suis emballé un peu vite (une fois de plus...)
Merci

[Joker62]

Soit
On se propose de dériver f.

On trouve :
Et on remarque que :



D'où

Et là t'as une équa diff

[fahr451]

joker un ' n 'aurait il pas sauté empêchant d'avoir cette équa diff?

[Joker62]

Bé euhhhh, si c'est valable pour tout x dans R, on peut pas s'arranger ensuite pour trouver les solutions pour x naturel ???

Enfin je sais pas xD tampis j'aurais essayer :(

[fahr451]

Soit
Et on remarque que :

je n 'arrive pas à le remarquer.

[Joker62]

Ah oui j'ai fait sauté un prime plutôt... j'vais voir ça

[Joker62]

Bonjour tout le monde
Donc voilà j'ai un début de proposition.

Donc on a :



Et plus généralement


On dérive les deux membres





D'où
En particulier pour
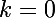
On trouve

Donc la solution est dérivable en 0 et sa dérivée vaut 4
Ce qui bannît donc la solution

Donc voilà dîtes moi quoi pour voir

[Joker62]

Je rectifie car je viens de comprendre que la solution proposée par fahr était pour le deuxième exemple :)
Donc désolé d'avoir bannît ta soluce ! :)

[fahr451]

Bonjour tout le monde




On dérive les deux membres

[

REM 1 on ne dérive que si on peut dériver donc si l'énoncé a précisé f dérivable

REM 2 si tel est le cas en dérivant ( n étant supposé réel car si n n'est qu'entier on ne peut pas directement le faire) par rapport à n , en n = 0 on trouve directement f ' (0) = 4

[Joker62]

Ah... c'est vrai que d'une on parle pas de dérivabilité
Et de deux, comme tu le dis n est entier donc oui ça marche po

Bon tampis :D si on trouve la soluce j'aimerai bien la voir lol parce que j'y pense quand même tout les jours c'est embêtant