Calcul matriciel

[yocto]

Bonjour à tous,

Voila j'ai des difficultés à résoudre un problème :

Soit la matrice A=
1 2 3
2 3 1
3 1 2

On demande d'abord de vérifier que (A-6I)(A²-3I)=0 ... ça pose pas de problème

C'est après que je bloque :
-Soient n N et le polynome de degrés <=2 tel que :

Je dois montrer que
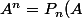-Meme question pour n Z

Merci pour votre aide

[Joker62]

Diagonalise d'abord A
Tu pourras déjà exprimé les puissances de A en fonction d'une matrice diagonale

[fahr451]

tu(ou quelqu'un d 'autre) a(s) déjà posé cette question

j (et d autres ) y ont déjà répondu
division euclidienne reste etc

[yocto]

ah ok j'vais aller y faire un tour.
nan nan j'm'amuse pas à poser 20 fois les mêmes kestions :marteau:

[fahr451]

écrivons la division euclidienne de X^n par (X-6)(X^2-3)

X^n = (X-6)(X^2- 3)Q(X) +Pn(X) avec Pn de degré 2 (*)

en substituant A à X on obtient

A^n = Pn(A)
et en évaluant (*) en 6 et rac(3) on obtient les relations demandées

[yocto]

merci fahr, mais avec Z, c koa la différence essentielle ?

[fahr451]

ha oui X^n n négatif n'étant pas un polynome on ne peut plus parler de division euclidienne faut ruser là

[fahr451]

alors on fait la même chose avec A^(-1) = B

de (A-6I)(A^2 -3I) = 0 on en déduit

(I-6B)(I-3B^2) = 0

on fait la division de X^n (n positif) par

(1-6X)(1-3X^2) = C

X^n = C(X)Q(X) + P(-n)(X) (*) deg P(-n)=<2

d'où

B^n = A^(-n) = R(B)


or en évaluant en 1/6 et +-1/rac(3)
on constate que P(-n) vérifie les relations demandées.

[fahr451]

c'est plus subtil je trouve

on pose B = A^-1

on a (A-6I)(A^2- 3I) = 0 = C(A) on en déduit deux choses

(I-6B)(I-3B^2) = 0 (en simplifiant par A^3)
soit L(B) = 0 avec L(X) = (1-6X)(1-3X^2)
et aussi :A^3 -6A^2- 3A = -18 I (en développant) soit

A^(-1) = (A^2 -6A- 3I)(-18) = K(A) avec K(6) = 1/6 et
K(rac(3)) = 1/rac(3) idem avec -
on fait avec B comme avec A
n positif
X^(n) = Q(X)L(X) +Rn(X) degRn=<2
donc B^n = Rn(B)
on a 6^n = Rn(1/6) idem avec les rac(3)
soit A^(-n) = Rn(A^-1) = Rn(K(A)) = Rn°K (A)
et on a bien Rn°K(6) = Rn(1/6) = 1/6^n
mais Rn°K est de degré 4 reste à faire la division euclidienne de Rn°K par C

Rn°K = Q1(X)C(X) +P(-n)
d'où A^(-n) = P(-n) (A)
et le P(-n) va bien :bonnes valeurs et bon degré.

(y a plus simple j'imagine)