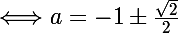Je viens de relire entièrement ce fil : je pense que cette remarque mérite un commentaire.
Je rappelle que la résolution d'une équation du second degré passe par la mise de cette équation sous forme canonique. On part de la forme :

On met a en facteur :

Puis on remarque que

est le début du développement du carré de
)
:
^2 = x^2+\frac{b}{a}x+\frac{b^2}{4a^2})
Par conséquent :
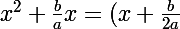^2 -\frac{b^2}{4a^2})
En reportant cette expression dans l'équation

on obtient :
^2 -\frac{b^2}{4a^2}+\frac{c}{a}]=0)
soit :
^2 -\frac{b^2-4ac}{4a^2}]=0)
Si le discriminant

est positif, c'est alors le carré de

et le premier membre de l'équation
^2 -\frac{b^2-4ac}{4a^2}]=0)
est une différence de deux carrés :
^2 -(\frac{\sqrt{\Delta}}{2a})^2]=0)
qui se factorise donc aisément :
 +(\frac{\sqrt{\Delta}}{2a})]\times [(x+\frac{b}{2a}) -(\frac{\sqrt{\Delta}}{2a})]=0)
d'où les deux solutions...
Il faut donc garder à l'esprit que la transformation de cette équation, l'utilisation du discriminant
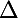
, n'a pour seul et unique but que de mettre le trinôme sous la forme d'une différence de deux carrés (ou d'une somme de deux carrés si

), c'est-à-dire sous la forme canonique :
^2+K] = 0)
ou
^2+K = 0)
Par conséquent, lorsque l'équation est déjà sous cette forme :
^2-2=0)
, il n'est pas vraiment raisonnable de développer et ensuite d'utiliser le discriminant pour remettre sous cette forme !
^2 -2=0)
^2=2)
^2=\frac{1}{2})
=\pm \frac{1}{\sqrt{2}})
=\pm \frac{\sqrt{2}}{2})