Problèmes de suites (terminale S)

[Makkai]

Bonsoiir

Haaa je sais normalement les suites c'est facile mais là je bloque. :cry:

La suite (Un) est définie par U0=1 et quelque soit n appartenant à N, U(n+1)=(1/2)Un+n-1.

1.a. Démontrer que pour tout n>(ou égal) 3, Un>(ou égal) 0
b. En déduire que pour tout n>(ou égal) 4, Un>(ou égal) n-2
c. en déduire la limite de la suite (Un)

2. On définit la suite (Vn)=4Un-8n+24
a. Démontrer que (Vn) est une suite géométrique décroissante dont on donnera la raison et le premier terme.
b. Démontrer que quelque soit n appartenant à N, Un=7(1/2)^n +2n-6

Je donne que le début parce que j'arriverais bien arriver à la fin par moi-même, un peu de fierté que diable :ptdr:

[annick]

Bonsoir,
pour la première question je verrais bien une démonstration par récurrence en posant un>0

[Makkai]

Vouip j'ai essayé mais ça ne marche pas je tome sur Un+1>n-1...

[annick]

je crois que si : un>=0 vrai pour u0
un+1=1/2un +n-1, avec un>=0 donc 1/2 un ausii et n>3 donc n-1>2 donc n-1>0

[Makkai]

Mais si on a n-1>0, on peut écrire n>0, d'accord, mais il manque l'expression de Un+1 non? On devrait pas tomber sur Un+1>0? Ca suffit vraiment, n-1>0?

[annick]

pour un+1>+0 sachant que un+1 est la somme de deux fonctions positives (un positif puisqu'on part de cette propriété et n-1 positif comme démontré précedemment), alors un+1 ne peut être que positif

[Makkai]

D'accord, j'ai compris... et pour le 1.b.?

[annick]

ça doit être tout bête car on demande de déduire, mais pour le moment je ne vois pas bien

[lexot]

Bonjour

donc >= 0 pour n >= 3

>= 0 avec n -1 >= 2

Ajoutons les 2 inégalitès :
+ n -1 >= 2 ou + n -1 >= 0

donc >= 0

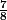
Alors >= 0 pour n = 3, car u3 = , et pour tout n de N.

Cordialement