Soient
Montrer qu'alors :
Bonne réflexion...
3) Inégalité à démontrer
5 messages
- Page 1 sur 1
3) Inégalité à démontrer
par nekros » 14 Jan 2007, 13:14
Salut :we:
Soient
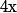
et 
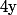
deux réels strictements positifs tels que 
Montrer qu'alors :^2 + (y+\frac{1}{x})^2 \ge \frac{289}{8}})
Bonne réflexion...
Soient
Montrer qu'alors :
Bonne réflexion...
par khaclong » 14 Jan 2007, 17:09
Salut!J'ai une autre solution pour ce problème
On a
^2 + (y+ \frac1x)^2=(x^2+y^2)(1+\frac{1}{(xy)^2})+2(\frac xy+\frac yx))
Ensuite, on utilise les inégalités
^2=32)
^2\geq xy)
Donc,
On a^2 + (y+ \frac1x)^2 \geq \frac{289}{8})
on admet Min quand x=y=4
On a
Ensuite, on utilise les inégalités
On a
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :