Matrice symétrique

[ludwig]

J'ai cette question à résoudre:
--> En déduire que si A est symétrique alors il en va de même de A², et plus généralement de A^K (avec k appartien à N*)
Donc si A est symétrique alors A² est symétrique car A^T*A^T =(A²)^T, mais comment montrer qu'il en va de même pour A^K ? il s'agit de le montrer avec un raisonnement par récurrence, qqn pourrait m'indiquer le détail de ce raisonnement ?

[tize]

Bonjour,
tu as essayé par récurrence... :we:

[Flodelarab]

G rien compris à ta première étape mais bon, pour la récurrence, regarde:

• Au rang 1: et sont elles symétriques ? Oui
• On suppose que si est symétrique, est symétrique
• Est ce vrai pour et ?

[ludwig]

En fait, je suis juste en science éco, et j'ai jamais fais un raisonnement par récurrence. Le prof n'a pas corrigé cette question et je ne suis pas capable de le faire...

[yos]

Hypothèse de l'exercice : A est symétrique.

Hypothèse de récurrence : k est un entier >0 tel que est symétrique. Alors donc est symétrique.

[tize]

Voila comment marche un raisonnement par récurrence :
Tu as une propriété que l'on va appeler et tu veux montrer qu'elle est toujours vrai quelque soit n.
Premièrement tu montres qu'elle vraie pour n=1
Ensuite tu fais comme si elle est vrai à un rang n quelconque et à partir de la tu essaies de montrer qu'elle est vraie au rang suivant : n+1.
Ensuite on peut conclure en disant qu'elle est vrai au rang 1 et que si elle est vraie au rang n alors elle l'est aussi au rang suivant, elle est donc vraie pour tout n.
Explicitement dans ton exemple ça donne ceci :
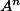: est symétrique
Pour n=1 :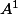 c'est évidement vrai.
Suppose que c'est vrai à un rang n :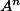 est symétrique, montrons que c'est vrai au rang n+1 : (car on a supposé 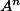symétrique) .
Ensuite on peut conclure...

[ludwig]

OK, je te remerci pour ta pédagogie.