[SECONDE] Exercice sur les vecteurs

[eorlan]

Bonsoir a tous

J'ai un DM à rendre pour demain et il me reste un dernier exercice qui me semble plutôt compliqué.. :hein:

J'ai seulement réussi a faire la figure et veuillez m'escuser de ne pas avoir de scanner pour vous la montrer ..

Voici l'énoncé :

ABCD est un parallèlogramme de centre O. Les points M,N,P et Q sont tels que :

(ce sont tous des vecteurs)

AM = 3/2 de AB
BN = 3/2 de BC
CP = 3/2 de CD
DQ = 3/2 de DA

1.)

a. Demontrez que MB = DP ( ce sont encore une fois des vecteurs )
b. Déduisez-en que O est milieu de [NQ]

2.)

Démontrez de même que O est milieu de [NQ]

3.)

Déduisez-en la nature de quadrilatère MNPQ.

Voilà.

PS : Merci a tous pour votre lecture, je ne demande pas forcément de réponses mais surtout des pistes car dès la première question.. je bloque ..

[Zebulon]

Bonsoir et bienvenue sur le forum !

Démontrer que

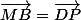
Par la relation de Chasles, on a : .
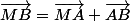
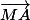
Remplace par quelque chose en fonction de ,
et comme ABCD est un parallélogramme, ...?
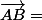
Je ne t'en dis pas plus, je te laisse chercher...

[eorlan]

En développant MB :

MB
= MA + AB
= MB + BA + AB
= MB

Heu ... Je tourne en rond non ?

[Zebulon]

En développant MB :

MB
= MA + AB
= MB + BA + AB
= MB

Heu ... Je tourne en rond non ?

Oui ! :we:
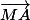
Exprime en fonction de .

[eorlan]

Je ne comprend pas comment faire ...

Voici la figure

[Zebulon]

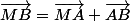
On dit dans l'énoncé que ,
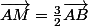
donc ?
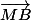
Et donc = (en fonction de ) ?
Ensuite, comme ABCD est un parallélogramme, .
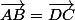
On remplace, et on y est presque.

[eorlan]

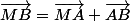
On dit dans l'énoncé que ,
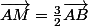
donc ?
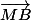
Et donc = (en fonction de ) ?
Ensuite, comme ABCD est un parallélogramme, .
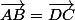
On remplace, et on y est presque.

hum ...

J'arrive donc à : MB = -1/2 de AB

...

Ensuite on peut alors dire MB = -1/2 de DC ...

Heu c'est le résultat nan ?

[Zebulon]

J'arrive donc à : MB = -1/2 de AB

Ensuite on peut alors dire MB = -1/2 de DC ...

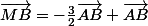
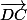
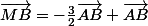
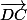
C'est ça. Je suppose que tu es passé par et qu'à ce moment tu as additionné puis remplacé par . Le plus jusdicieux est de rester à cette forme () et de remplacer par . On voit alors apparaître un , ce qui s'écrit aussi et peut être utile...

[eorlan]

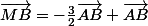
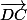
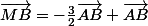
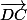
C'est ça. Je suppose que tu es passé par et qu'à ce moment tu as additionné puis remplacé par . Le plus jusdicieux est de rester à cette forme () et de remplacer par . On voit alors apparaître un , ce qui s'écrit aussi et peut être utile...

En effet

Merci beaucoup a toi je dois pouvoir finir cette question tout seul je pense

PS : Merci aussi de la gentillesse avec laquelle tu m'a répondu

[Zebulon]

Merci beaucoup a toi
PS : Merci aussi de la gentillesse avec laquelle tu m'a répondu

De rien ! C'est un plaisir d'aider ceux qui le demandent poliment (et vous remercie en plus ! :we: )

je dois pouvoir finir cette question tout seul je pense

Parfait ! Mais je pense que tu t'es trompé en recopiant le sujet : ça doit être "Déduisez-en que O est le milieu de [MP]", [NQ] c'est pour la 2ème question.

Bon courage et n'hésite pas à redemander de l'aide si ça coince !:happy3:

[eorlan]

Oui en effet je me suis trompé mais tu m'a bien corrigé ;)

Merci je n'hesiterais pas ;)

[eorlan]

Oulaa ...

Bon apparament je n'arrive toujours pas a trouver la réponse a la deuxieme question du 1°) qui je rappelle est :

Déduisez en que O est le milieu de [MP]

J'ai 2 pistes :

Essayer de montrer que PO = 1/2 de PM
ou encore PO + BO = Vecteur nul ..

[Zebulon]

D'une manière générale, comment montrer que I est le milieu de [EF] ? On peut peut montrer par exemple que .
Alors ici, qu'est-ce qu'on pourrait montrer comme égalité vectorielle ?

[eorlan]

D'une manière générale, comment montrer que I est le milieu de [EF] ? On peut peut montrer par exemple que .
Alors ici, qu'est-ce qu'on pourrait montrer comme égalité vectorielle ?

Je crois qu'essayer de montrer que PO=OM doit etre faisable ...

J'essai ... :id:

[eorlan]

Je suis sur la bonne piste !!

Exemple :

PO = OM

PD + DO = OB + BM

On vient de montrer que DP = MB

Donc ils s'annulent et il nous reste : DO = OB et comme c'est un parallèlogramme, en effet DO = OB ...

L'égalité est alors démontré ..


- Correct ? -

[Zebulon]

J'ai 2 pistes :

Essayer de montrer que PO = 1/2 de PM
ou encore PO + BO = Vecteur nul ..

Si tu modifies tes messages pendant que je réponds !
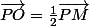
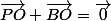
Oui, pour , non pour . (OK si changes rapidement ton B en M)
Calcule en introduisant, par la relation de Chasles, les points D et B, et en te souvenant que dans un parallélogramme, le centre est le millieu des diagonales.

[Zebulon]

Avec les deux liaisons en rouge, j'aime mieux ! :we:

PO = OM
PD + DO = OB + BM
Or On vient de montrer que DP = MB
Donc ils s'annulent et il nous reste : DO = OB et comme c'est un parallèlogramme, en effet DO = OB ...
L'égalité est alors démontrée ..
- Correct ? -

Mais le raisonnement est tout à fait correct ! :++:

[eorlan]

Oups désolé pour les fautes mais bon le soir a 23h31 en plein DM de maths ... :dodo:

Merci pour les informations, je viens de rédiger tout ca.

Cependant désolé de t'embeter encore mais pour la question suivante ( Trouvez ensuite que O est le milieu de [NQ] ), il faut que je refasse TOUT ?! :marteau:

[Zebulon]

il faut que je refasse TOUT ?! :marteau:

Tout ? Oui, mais ça ne prend que quelques lignes ! C'est la même chose chose, bien que diamètralement opposée ! :ptdr:
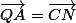
Commence par montrer que , puis déduis-en etc...

[eorlan]

Bon bah je me relance dedans :D