Matrice inversible
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 17:23
par ludwig » 07 Jan 2007, 17:23
Bonjour,
L'énoncé de mon exo est le suivant: Si les matrices a et b sont inversibles, montrer que l'on a l'équivalence (ab)²=a²b² équivaut à ab=ba
Donc on aurait (ab)(ab)=aabb donc comme a est inversible: a^-1(ab)(ab)=a^-1aabb donc Ibab=Iabb et comme b est inversible: donc Ibabb^-1=Iabb^-1 donc IbaI=IabI donc ba=ab. Le raisonnement est-il correct ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Jan 2007, 17:25
par tize » 07 Jan 2007, 17:25
Bonsoir,
oui, ça me semble correct et dans l'autre sens ab=ba => (ab)²=a²b²
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 07 Jan 2007, 17:40
par simplet » 07 Jan 2007, 17:40
oui c bon. pour l'autre sens il n'y a quasi rien a dire, un seul signe égal suffit :-)
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 17:40
par ludwig » 07 Jan 2007, 17:40
Oui, les deux sens sont justes et démontrables. Par contre si j'ai une matrice carrée telle que A^k + C (indice K-1)*a^K-1+....+c(indice1) *A + C(indice0)* I =0 ; comment puis montrer que A est inverser pour ensuite donner une expression de A^-1 ?
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 07 Jan 2007, 17:45
par jose_latino » 07 Jan 2007, 17:45
À partir de
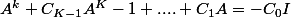
, factorise

à gauche et passe à diviser

qui est différent de 0 (justifier)
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 18:00
par ludwig » 07 Jan 2007, 18:00
Donc en quoi le fait d'écrire: (expression de A) A /-C0 =I montre que a est inversible ?
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 18:06
par ludwig » 07 Jan 2007, 18:06
Suffit de dire que A^-1= (expression de A factorisé)/-C0
? et comment tu factorises A ?
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 07 Jan 2007, 18:14
par jose_latino » 07 Jan 2007, 18:14
jose_latino a écrit:À partir de
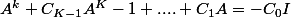
, factorise

à gauche et passe à diviser

qui est différent de 0 (justifier)
donc
]=I)
, ça veut dire que
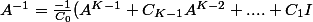)
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 07 Jan 2007, 18:18
par jose_latino » 07 Jan 2007, 18:18
ludwig a écrit:Donc en quoi le fait d'écrire: (expression de A) A /-C0 =I montre que a est inversible ?
C'est possible démontrer que s'une matrice carrée a une inverse à droite ( à gauche), celle-ci est une inverse à gauche (respectivement à droite). Une façon plus courte de dire tout ça c'est la suivante:
Pour des matrices A et B, carrée et du même ordre, ces sont équivalentes:
- B est l'inverse à droite de A
- B est l'inverse à gauche de A
- B est l'inverse de A
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 18:36
par ludwig » 07 Jan 2007, 18:36
Très bien, j'ai noté. Encore une question:je veux montrer que si A et B sont deux matrices symétriques qui commutent alors AB est aussi une matrice symétrique.
Je fais: si A^T*B^T= B^T *A^T donc AB = (AB)^T
Ensuite j'en déduis que si A est symétrique alors A² est symétrique car A^T*A^T =(A²)^T, mais comment montrer qu'il en va de même pour A^K ?
-
ludwig
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Avr 2006, 19:20
-
 par ludwig » 07 Jan 2007, 19:08
par ludwig » 07 Jan 2007, 19:08
personne pour m'aider ?
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 07 Jan 2007, 21:44
par jose_latino » 07 Jan 2007, 21:44
Tout le monde est en vacances, except moi je crois :we:
Pour le problème en général fais une démonstration par récurrence. C'est presque la même idée que pour le cas n=2 (que tu as déjà fait)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
