Produit maximal

[BancH]

Voici un exercice d'olympiades dont j'ai modifié l'énoncé pour le généraliser.

Soit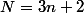 un entier positif, déterminer le plus grand nombre étant le produit d'entiers positifs dont la somme est égale à .

[namfoodle sheppen]

Soit S un ensemble de nombres entiers dont la somme est égale à N et dont le produit est maximal. On peut supposer que tous les éléments de S sont égaux à 2 ou 3 (en effet si on prend y€S, y>3, 2*(y-2)>=y, donc le produit est supérieur en remplacant y par (y-2,2) dans S).
Montrons maintenant que S est composé exclusivement de 3 excepté un élément. En effet S comprend forcement un 2, car N n'est pas un multiple de 3. Supposons par l'aburde que S comporte plus d'un 2. Alors le nombre de 2 appartenant à S est congru à 1 modulo 3. Comme 2^3<3^2, il y a contradiction avec le fait que S est maximal.
S est donc composé de n 3 et de un 2. Le produit est alors 3^n*2.

[BancH]

Ouais bien joué, c'est exactement ça. Le plus difficile était de montrer que 3 était le facteur maximisant le produit.

[BancH]

si on prend y€S, y>3, 2*(y-2)>=y, donc le produit est supérieur en remplacant y par (y-2,2) dans S

Moi j'avais pensé à maximiser dans , ou plus simplement dans , mais je ne trouve pas de méthode pour le faire.

A moins de faire comme toi, de supposer que est maximisant, et de voir que l'inégalité suivante n'a pas de solutions :



Pour l'inégalité n'est pas respectée, et quand augmente de , le numérateur du membre de droite augmente d'au moins tandis que son dénominateur augmente seulement de . Lorsque augmente le membre de droite augmente, donc quelque soit entier, l'inégalité n'est pas respectée et est donc le facteur maximisant le produit sur .

Et comme , on conclut.

Mais bon, j'aurais aimé ne pas avoir à faire de supposition.

[BiZi]

Est-il possible d'avoir la source de cet exercice? olympiade internationale? académque? année?

[BancH]

J'ai légèrement modifié l'énoncé, c'est un olympiade international de 1976.

Pourquoi as-tu besoin des sources, pour chercher la solution ou par convention?

[BiZi]

J'ai légèrement modifié l'énoncé, c'est un olympiade international de 1976.

Pourquoi as-tu besoin des sources, pour chercher la solution ou par convention?

Merci. Pour répondre à ta question, c'est toujours intéressant de savoir à quoi on s'attaque.

[BancH]

Si je le remodèle entièrement, besoin des sources quand même?

Par exemple le problème d'origine c'est précisément :

"Déterminer le plus grand nombre qui est le produit d'entiers positifs dont la somme est 1976."


Mais maintenant je peux dire :

J'ai pièces de monnaie, je veux en faire un certain nombre de tas tel que le produit de leurs hauteurs soit maximal, comment dois-je m'y prendre?

[e^x]

Bonjour à tous!

Voilà, je ne saisis pas tout à fait le problème:
J'arrive à quelque chose qui n'a rien à voir... Les conditions pour que n soit correct sont que:

N-2=3n
n=ab
a+b=N

-> n>= -2/3 -> 3n>= -2

N-2=3ab
N=a+b
(3ab=a+b-2)>= -2
a+b>=0

Où me suis-je trompé?

[BancH]

C'est quoi ton problème, a+b>0? Tu pensais directement trouver le résultat?

[e^x]

Non, mais cela signifierait que n peut prendre pratiquement n'importe quelle valeur, il suffit que a+b soit positif et ensuite on fait le produit des deux termes???

Serait-ce une mauvaise interprétation du problème?
Confusion de N et n?

[BancH]

Dans tes calculs tu n'as pas traduit le fait que et doivent maximiser le produit.

Par exmple avec N=8

Tu peux faire

1x1x1x1x1x1x1x1
2x2x2x2
5x3
6x2
4x4
....

Et il faut trouver le plus grand produit.

[e^x]

Ca m'avais complètement échappé!
Merci beaucoup!