Problème en algèbre!

[cece71]

J’ai un gros problème sur un exercice,en voici l’énoncé :
Soit P(X)= ;)(k=0 à p) a indice k*X^k appartient a C(X) de degré p>0
Et Q(X)=;)(k=0 à q) b indice k*X^k appartient a C(X) de degré q>0
On note R(P(X),Q(X)) le dét de la matrice carrée de taille p+q :
a0 0 ….. 0 b0 0 …0
a1 a0 0 : b1 b0 :
: a1 a0 0 : b1 . 0
: : a1 a0 : : b1 b0
ap : a1 bq : b1
0 ap : 0 bq :
: 0 ap : : 0 bq :
0...0 ap 0...0 bq
;) q ;) ;) p ;)
colonnes colonnes

1) il faut montrer que P(X) et Q(X) ont un facteur commun de degré ;) 1 ssi ils ont au- une racine en commun.
2) Il faut montrer que P(X) et Q(X) ont un facteur commun de degré ;) 1 ssi il existe des polynomes complexes P1(X) et Q1(X) tels que deg(P1(X))3) Déduire que P(X) et Q(X) ont un facteur commun de degré ;) 1 ssi P(X), XP(X), …,X^(q-1)P(X), Q(X),….., X^(p-1)Q(X) est une famille liée.
4) Déduire que P(X) et Q(X) ont au- une racine commune ssi R(P(X),Q(X))=0

Merci de m’aider…

[tize]

Pour la 1) il y a un théorème qui dit que dans C[X] si a est une racine d'un polynome P alors (X-a) divise P... tu te sers de ça pour décomposer un polynome en produit de facteurs de degré 1 et faire la 2. et 3 grâce à 2 avec des combinaisons linéaires...

[cece71]

J'ai pas bien compris comment on pouvait décomposer P et Q en produit de facteurs premiers grâce a ce théorème?

[tize]

Connais tu le théorème de D'Alembert-Gauss ?http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_d%27Alembert-Gauss

[cece71]

A merci!!!Je connaissais le théorème, mais je ne connaissais pas la démonstration!Merci encore! Et donc grâce à cà je vais pouvoir répondre 2 et 3?

[tize]

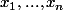
Ba ça va beaucoup t'aider car ça te permet de dire par la suite que pour tout polynome P de C[X] de degre n il existe n racines de P et un coefficient a tels que

[cece71]

5) Montrer que les racines de P(X) st simples ssi D(P(X))=R(P(X),P'(X)) est différent de 0
6) Soit a(Y) appartient a C(Y) et Q(Y)=R(P(X),X-a(Y))
Montrer que y est racine de Q(Y) ssi a(y) est racine de P(X)
7)Soit a(X) appartient C(X) et Q(Y)=R(P(X),a(X)-Y)
Montrer que, si x est une racine de P(X), alors y=a(x) est une racine de Q(Y)

Merci de m'aider pr ce problème

[cece71]

personne a une petite idée qui pourrait me guider???

[tize]

pour la 5), si tu as fait ça :

4) Déduire que P(X) et Q(X) ont au- une racine commune ssi R(P(X),Q(X))=0

alors c'est simple car si b est une racine double de P alors c'est aussi une racine de P' (en effet (x-b)^2 divise P...)

[yos]

Note culturelle :
Le déterminant R(P,Q) est le résultant des polynômes P et Q. Il est aussi égal au produit des valeurs de P en les racines de Q et donc aussi au produit des valeurs de Q en les racines de P (au signe près).
Quand à R(P,P') c'est le discriminant de P (au signe près).