Question sur les majorants
9 messages
- Page 1 sur 1
Question sur les majorants
Bonjour, pour le c) et le d) je ne comprends pas pourquoi pour cette ensemble on parle de majorants supérieurs à 1 puisqu'il est défini avec K appartenant à N sauf 0 il ne devrait pas y avoir de majorant supérieur à 1 ou ai-je mal compris quelque chose ?


Re: Question sur les majorants
Salut,
Pour le (c) (par exemple), ton ensemble, c'est l'ensemble des "trucs" qui peuvent s'écrire sous la forme 1/k avec k dans N*, c'est à dire 1, 1/2, 1/3, 1/4, . . .
Et très clairement, à part 1, ces "trucs ne sont pas des entiers, mais des rationnels. Et il est tout aussi clairement, le nombre 1 est le plus grand de tous et c'est donc le maximum de l'ensemble donc aussi la borne supérieure ce qui signifie que les majorants de l'ensemble sont précisément les réels supérieurs ou égaux à 1.
Et, d'un autre coté, tout les nombre de l'ensemble sont évidement >0 donc 0 est un minorant de l'ensemble et c'est le meilleur vu que pour tout a>0, il va exister un k entier tel que 1/k<a donc a n'est pas un minorant de l'ensemble. Le nombre 0 est donc le plus grand minorant, c'est à dire la borne inférieure de l'ensemble. Et comme il n'appartient pas à l'ensemble, c'est que l'ensemble n'admet pas de minimum.
Pour le (c) (par exemple), ton ensemble, c'est l'ensemble des "trucs" qui peuvent s'écrire sous la forme 1/k avec k dans N*, c'est à dire 1, 1/2, 1/3, 1/4, . . .
Et très clairement, à part 1, ces "trucs ne sont pas des entiers, mais des rationnels. Et il est tout aussi clairement, le nombre 1 est le plus grand de tous et c'est donc le maximum de l'ensemble donc aussi la borne supérieure ce qui signifie que les majorants de l'ensemble sont précisément les réels supérieurs ou égaux à 1.
Et, d'un autre coté, tout les nombre de l'ensemble sont évidement >0 donc 0 est un minorant de l'ensemble et c'est le meilleur vu que pour tout a>0, il va exister un k entier tel que 1/k<a donc a n'est pas un minorant de l'ensemble. Le nombre 0 est donc le plus grand minorant, c'est à dire la borne inférieure de l'ensemble. Et comme il n'appartient pas à l'ensemble, c'est que l'ensemble n'admet pas de minimum.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Question sur les majorants
C'était exactement mon raisonnement mais dans le correctif l'assistante a suggéré comme ensemble des majorants l'ensemble [1,+inf[, je poste ici plus bas la photo du correctif, serait-ce une malencontreuse erreur ou j'ai mal interpreté quelque chose?
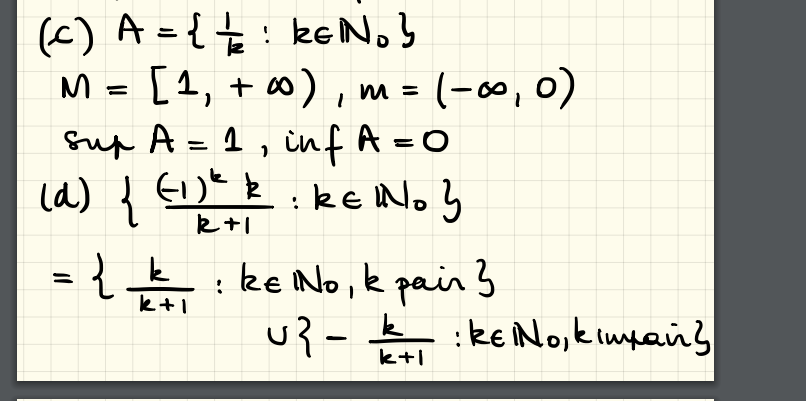
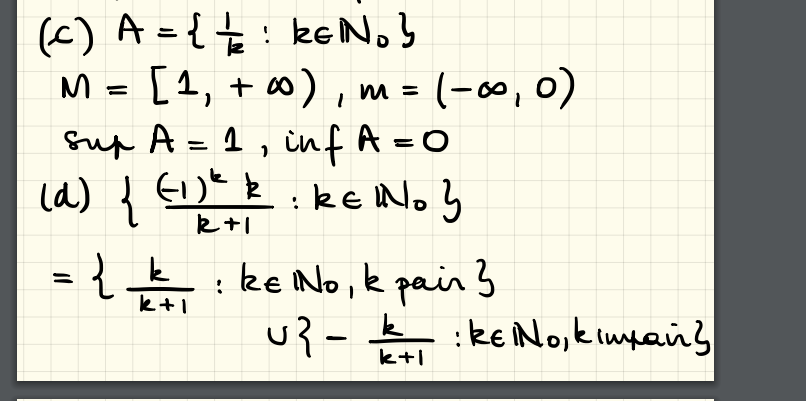
Re: Question sur les majorants
Bonjour
Je pense que tu as mal interprété le message de Ben314 pourtant on ne plus clair, je cite :
donc situés dans l'intervalle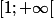
Je pense que tu as mal interprété le message de Ben314 pourtant on ne plus clair, je cite :
1 est le plus grand de tous et c'est donc le maximum de l'ensemble donc aussi la borne supérieure ce qui signifie que les majorants de l'ensemble sont précisément les réels supérieurs ou égaux à 1
donc situés dans l'intervalle
Re: Question sur les majorants
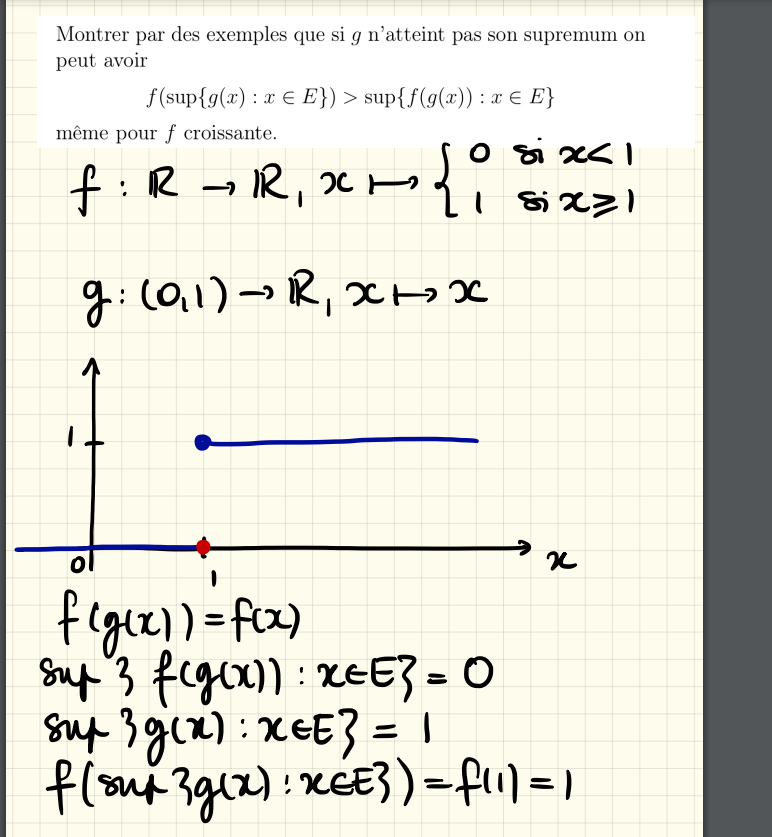
Dans le même thème, pourrais-t-on m'expliquer pourquoi le supremum de f°g est 0, question toute bête mais qui m'échappe ...

Re: Question sur les majorants
Bonjour
Je suppose que (0,1) est l'intervalle ]0;1[ (en notation anglaise), je pense aussi que E contient ]0;1[ ou lui est égal.
donc la borne sup de {g(x), x élément de E} est bien 1
mais si on calcule fog(x) avec x dans E, c'est égal à f(x) avec x<1 donc fog(x)=0 pour tout élément x de E et la borne sup de {fog(x), x élément de E} est 0.
Je suppose que (0,1) est l'intervalle ]0;1[ (en notation anglaise), je pense aussi que E contient ]0;1[ ou lui est égal.
donc la borne sup de {g(x), x élément de E} est bien 1
mais si on calcule fog(x) avec x dans E, c'est égal à f(x) avec x<1 donc fog(x)=0 pour tout élément x de E et la borne sup de {fog(x), x élément de E} est 0.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :