Term S(spé)2004 la Réunion pour un DM

[indochinoiz]

bonjour à tous je suis à la recherche du corrigé de l'exercice de spécialité du bac 2004 La Réunion.Ou de l'aide car je n'arrive que la question 1!
on peut trouver le sujet à partir de ce lien:
http://perso.orange.fr/apmep_reunion/bac%20session%20anterieures.htm

[fonfon]

Salut,

1a.

on te donne le petit theoreme de Fermat,donc d'apres celui-ci si p est un nombre premier et si a est premier avec p alors:
est divisible par p.
l'entier p est 1er et impair donc p est 1er avec a=2 donc est divisible par p donc:



de plus p est un nombre premier impair donc donc on en deduit que p-1 est non nul

alors
si p est un nombre 1er impair, alors il existe un entier naturel k (non-nul)tel que k=p-1 et donc

voilà A+

[indochinoiz]

Merci!mais j'avais omis de précisé que c'était la seule question que j'avais réussi.

[indochinoiz]

help :cry:

[indochinoiz]

desespoire de trouver ce corrigé... :cry2:

[indochinoiz]

voici l'énoncé:

On rappelle la propriété, connue sous le nom de petit théorème de Fermat :
« soit p un nombre premier et a un entier naturel premier avec p ;alors a^ (p-1)-1
est divisible par « .
1. Soit p un nombre premier impair.
a. Montrer qu'il existe un entier naturel k, non nul, tel que 2^k congru 1 [p].
b. Soit k un entier naturel non nul tel que 2^ k congru 1 [p]et soit n un entier
naturel. Montrer que, si k divise n, alors 2^n congru 1 [p].
c. Soit b tel que 2 b congru 1 [p], b étant le plus petit entier non nul vérifiant
cette propriété.
Montrer, en utilisant la division euclidienne de n par b,que si 2^ n congru 1 [p], alors b divise n.
2. Soit q un nombre premier impair et le nombre A =2 ^(q- 1).
On prend pour p un acteur premier de A.
a. Justifier que : 2^q congru 1 [p].
b. Montrer que p est impair.
c. Soit b tel que 2^b congru 1 [p],b étant le plus petit entier non nul vérifiant
cette propriété.
Montrer, en utilisant 1. que b divise q. En déduire que b = q.
d. Montrer que q divise p -1, puis montrer que p congru 1 [p].
3. Soit A1 =2 17
1. Voici la liste des nombres premiers inférieurs `a 400 et
qui sont de la forme 34m+1, avec m entier non nul : 103, 137, 239, 307.
En déduire que A1 est premier.

[kikinette007]

j'aurais besoin d'aide sur l'exercice 4 s'il vous plait

[BancH]

C'est quoi au juste l'exercice 4?

[indochinoiz]

euh je ne sais pas mais je cherhce tjs de l'aide!pour la 1a c'est ok

[BancH]

Si divise , alors il existe un entier tel que

[indochinoiz]

Si divise , alors il existe un entier tel que

je ne vois pas à quelle question ceal correspond^^
j'ai besoin d'aide uniquement pour la question 2d et la 3

[BancH]

C'était la 1b.

[indochinoiz]

a merci mais j'ai réussi :id:
par contre si tu as une idée pour la 2 d et la 3!!je veux bien

[fonfon]

Salut,

d. Montrer que q divise p -1, puis montrer que p congru 1 [p].

je pense que c'est plutôt p congru 1[2q] non?
2.d

Si p est un entier premier impair, alors p et 2 sont premiers entre eux et on a (d'apres le petit theoreme de Fermat):
donc

or on sait que q est un entier qui verifie et q est egal au plus petit entier non nul verifiant et avec la propriete du 1. c on a q divise p-1.


de plus , p est impair donc p-1 est pair donc il existe un entier naturel m tel que p-1=2m.
Comme q divise p-1, q divise 2m; q etant 1er impair.
p est 1er avec 2 donc d'apres Gauss, q divise m donc m s'ecrit m=kq avec k entier naturel.
Donc

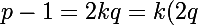donc




donc si p est un facteur premier de A=2^(q-1) (q 1er impair) alors p est 1er impair et on a

[indochinoiz]

euh oui dsl c'est bien 2q!!

merci bcp^^