Calcul d'une série entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
issoram
- Membre Relatif
- Messages: 100
- Enregistré le: 01 Déc 2020, 18:18
-
 par issoram » 22 Sep 2024, 16:20
par issoram » 22 Sep 2024, 16:20
Bonjour,
J'essaie de calculer cette série entière:
Pour
=\sum_{n\geq1}^{}{\frac{x^n}{n^2}}+\sum_{n\geq1}^{}{\frac{(1-x)^n}{n^2}})
En passant à la dérivée j'obtiens:
=\sum_{n\geq1}^{}{\frac{x^{n-1}}{n}}-\sum_{n\geq1}^{}{\frac{(1-x)^{n-1}}{n<br />}} = \frac{1}{x}\sum_{n\geq1}^{}{\frac{x^{n}}{n}}-\frac{1}{1-x}\sum_{n\geq1}^{}{\frac{(1-x)^{n}}{n<br />}}=-\frac{ln(1-x)}{x}+\frac{ln(x)}{1-x})
Mais ensuite je coince pour remonter à S(x) par intégration... Je me suis peut être trompé avant...
Merci de votre aide
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 23 Sep 2024, 11:35
par catamat » 23 Sep 2024, 11:35
Bonjour
Si on pose u(x)=lnx et v(x)=-ln(1-x)
S'(x)=u'(x)v(x)+u(x)v'(x) donc S=uv
-
issoram
- Membre Relatif
- Messages: 100
- Enregistré le: 01 Déc 2020, 18:18
-
 par issoram » 23 Sep 2024, 11:40
par issoram » 23 Sep 2024, 11:40
J'ai finalement réussi à intégrer, c'était juste la dérivée d'un produit!
Au final j'obtiens :
=-\ln(x)\ln(1-x))
Si j'évalue S en
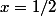
avec cette formule j'obtiens
^2)
Ce n'est pas cohérent car cette somme devrait être positive.
Il y a donc une erreur dans mon raisonnement, mais je ne la vois pas pour l'instant.
Modifié en dernier par
issoram le 23 Sep 2024, 11:43, modifié 1 fois.
-
issoram
- Membre Relatif
- Messages: 100
- Enregistré le: 01 Déc 2020, 18:18
-
 par issoram » 23 Sep 2024, 11:42
par issoram » 23 Sep 2024, 11:42
Merci Catamat, effectivement j'ai vu ça ce matin. J'essayais d'intégrer séparément les 2 fractions alors que la réponse était sous mes yeux...
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 23 Sep 2024, 18:39
par catamat » 23 Sep 2024, 18:39
Quand tu intègres la primitive est connue à une constante près....
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 23 Sep 2024, 18:51
par catamat » 23 Sep 2024, 18:51
D'autre part, le 1/x exclut la valeur 0 qui est valable au départ
-
issoram
- Membre Relatif
- Messages: 100
- Enregistré le: 01 Déc 2020, 18:18
-
 par issoram » 23 Sep 2024, 20:27
par issoram » 23 Sep 2024, 20:27
Merci Catamat, effectivement je fais les choses à moitié...
1)

est continue en 1 avec
 = \sum_{n=1}^{+\infty}{1/n^2}= \frac{\pi^2}{6})
2)
=-\ln(x)\ln(1-x)+C)
3) S étant continue en 1, en faisant tendre x vers 1 dans l'égalité précédente, on obtient:
 = \frac{\pi^2}{6})
Ainsi
 = -\ln(x)\ln(1-x)+\frac{\pi^2}{6})
4) Petite vérif pour
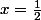
 = 2\sum_{n=1}^{+\infty}{\frac{1}{2^n n^2}}=-\ln(2)^2+\frac{\pi^2}{6})
Soit
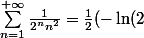^2+\frac{\pi^2}{6}))
Ce qui est vrai...
Je ne suis pas sûr de moi pour le point 3)... N'hésitez pas si je dis des bêtises...

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités