Salut !
Déjà un petit point méthode :
1. Pour montrer que

est bien un sous-espace vectoriel de

tu peux
seulement montrer que (

contient

évidemment et que)

, quels que soient

et le scalaire

: ça revient au même et ça évite d'avoir deux scalaires à manipuler.
2. Dans ton cours tu sais probablement que le noyau d'une application linéaire est un sous-espace vectoriel de l'espace de départ. Donc pour montrer que

est un sous-espace vectoriel de

il te suffit d'écrire

comme noyau d'une application linéaire. Par exemple pour le (i),

est le noyau de l'application linéaire

définie par
= 2x-y+z)
.
Pour ce que tu as fait, je n'ai pas tout compris... Si on reprends le (i), étant donnés
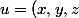\in F)
et
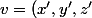\in F)
et
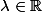
, il faut montrer que

, c'est-à-dire que
-( y+\lambda y')+(z+\lambda z')=0)
à partir du fait que
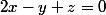
et

.
Même idée pour le (iii) : sachant que

et

, il faut montrer que
+i(y+\lambda y')=(z+\lambda z')-i(t-\lambda t')=0)
.
Autre méthodes :
- tu peux montrer que

où
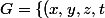 \in \mathbb{C}^4\ ;\ x+iy=0 \})
et
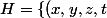 \in \mathbb{C}^4\ ;\ z-it=0 \})
sont deux sous-espaces vectoriels, et en déduire la conclusion souhaitée puisque l'intersection de deux sous-espaces vectoriels est un espace vectoriel.
- enfin, tu peux trouver une application linéaire

telle que
=F)
.


