Merci Ben.
Ah bin oui c'est bien plus rapide.
Concernant la question a) j'ai utilisé le théorème 2.2.c) :
ISOMÉTRIES, SIMILITUDES.Algèbre bilinéaire.
2.1. Définitions.
Définition 2.1. Soit

un espace vectoriel euclidien, et

un endomorphisme de

. On dit que

est orthogonal, ou une isométrie quand

conserve le produit scalaire
 \mid f(y))=(x \mid y) .)
On dit que

est une similitude de rapport
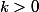
quand

"multiplie" le produit scalaire par

 \mid f(y))=k^2(x \mid y) .)
Théorème 2.1. Soit

un endomorphisme de l'espace euclidien

.
Les conditions suivantes sont équivalentes
(a)

est une isométrie;
(b) l'image d'une base orthonormale par

est une base orthonormale;
(c)

conserve la norme : pour tout vecteur
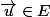
, on a
|=|\vec{u}|)
;
(d) la matrice de

dans une base orthonormale est orthogonale, c'est à dire qu'elle vérifie

.
Exercice 2.1. Montrer qu'une symétrie orthogonale est une isométrie.
Théorème 2.2. Soit

un endomorphisme de l'espace euclidien

.
Les conditions suivantes sont équivalentes
(a)

est une similitude de rapport

;
(b)

"multiplie" la norme par

: pour tout vecteur
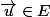
,
|=k|\vec{u}|)
;
(c) la matrice de

dans une base orthonormale vérifie

.