Série entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par matheuxendetresse » 01 Mai 2024, 18:08
par matheuxendetresse » 01 Mai 2024, 18:08
Bonjour,
Je voudrais savoir si mes résultats sont corrects, pour calculer la somme de cette série de rayon de convergence égal à

:
 = \sum_{n \geq 0} n^{(-1)^n} z^n)
Premièrement j'ai dérivé:
^n+1} z^{n-1})
Qui est égal à:
^2-1) z^{2n+1})
Pour

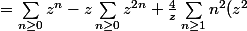^n)
}{(1-z^2)^3})
Et en intégrant:
 = \frac{z^2}{2(z^2-1)^2}-ln(1-z)- \frac{1}{2} ln(1-z^2))
Est-ce que ce que j'ai fait est correct?
MERCI!
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 01 Mai 2024, 21:07
par phyelec » 01 Mai 2024, 21:07
Bonjour,
Il faut calculer le rayon de convergence pour savoir dans quel intervalle se trouve z.
J'ai un doute sur la manière dont vous conduisez le calcul. Pour moi il fait étudier la somme S1 des éléments quand n est pair et la somme S2 des éléments quand la suite est impair. On a S=S1+S2
sauf erreur de ma part je trouve :
 =\dfrac{2z^2}{(1-z^2)^2} + \dfrac12 (ln(1+z) -ln(1-z)))

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Mai 2024, 21:31
par Ben314 » 01 Mai 2024, 21:31
Je trouve comme phyelec (modulo un +1 pour que la formule donne le bon terme constant) et ça semble être confirmé par
Wolfram Alpha (où on peut cliquer sur "more terms")
Modifié en dernier par
Ben314 le 01 Mai 2024, 21:45, modifié 5 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par matheuxendetresse » 01 Mai 2024, 21:34
par matheuxendetresse » 01 Mai 2024, 21:34
phyelec a écrit:Bonjour,
Il faut calculer le rayon de convergence pour savoir dans quel intervalle se trouve z.
J'ai un doute sur la manière dont vous conduisez le calcul. Pour moi il fait étudier la somme S1 des éléments quand n est pair et la somme S2 des éléments quand la suite est impair. On a S=S1+S2
sauf erreur de ma part je trouve :
 =\dfrac{2z^2}{(1-z^2)^2} + \dfrac12 (ln(1+z) -ln(1-z)))
Bonjour, merci.
En fait, j'ai mal intégré, j'ai réintégré mon expression, (je l'ai intégrée séparément et j'ai fais une erreur de signe et oublié de multiplié par 4) et cela a donné exactement ce que vous avez trouvé:
}{(1-z^2)^3} dz)
^2}-ln(1-z)+\dfrac{1}{2} ln(1-z^2))
^2} + \dfrac12 (ln(1+z) -ln(1-z)))
Pour le rayon de convergence c'est

(je l'avait écrit)
 par matheuxendetresse » 01 Mai 2024, 21:35
par matheuxendetresse » 01 Mai 2024, 21:35
Ben314 a écrit:Je trouve comme 'ai l'impression qu'il y a une erreur de calcul : vérifie avec par exemple Wolfram Alpha (fait un D.L. à l'ordre 7 ou 8 pour vérifier).
Perso, je trouve
=\dfrac{2 z^2}{\big(1 - z^2\big)^2} +\dfrac{1}{2}\ln\Big(\dfrac{1\!+\!z}{1\!-\!z})\Big))
Merci, oui, j'ai fait une erreur de signe et j'ai oublié de multiplié par

car j'ai intégré l'expression séparement

 par matheuxendetresse » 01 Mai 2024, 21:38
par matheuxendetresse » 01 Mai 2024, 21:38
Ben314 a écrit:Je trouve comme phyelec (modulo un +1 pour que la formule donne la bon terme constant) et ça semble être confirmé par
Wolfram Alpha
Et du coup, vous le faites par quelle méthode? je crains que ma méthode soit fausse même si les résultats sont bons.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Mai 2024, 21:44
par Ben314 » 01 Mai 2024, 21:44
J'ai fait comme toi à un mini détail prés : je n'ai pas "décalé" les indices dans la somme compliquée.
Et c'est parfaitement correct.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par matheuxendetresse » 01 Mai 2024, 21:50
par matheuxendetresse » 01 Mai 2024, 21:50
Ben314 a écrit:J'ai fait comme toi à un mini détail prés : je n'ai pas "décalé" les indices dans la somme compliquée.
Et c'est parfaitement correct.
Merci.
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 02 Mai 2024, 20:23
par phyelec » 02 Mai 2024, 20:23
Quelle méthode utilisée? les 2 méthodes me semblent viables.
J'ai l'impression que quand on scinde en 2 séries les calculs sont plus faciles:
^n})
, le rayon de convergence est 1. Donc converge dans l'intervalle ]-1,1[, en séparant impair et pair on a :
=\sum_{n=0}^{+\infty}\dfrac{z^{2n+1}}{2n+1} +\sum_{n=1}^{+\infty} 2n z^{2n}})
pour le terme

on dérive et on obtient :
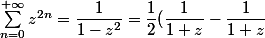)
on calcul la primitive :
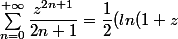-ln(1-z)))
pour l'autre terme on a :
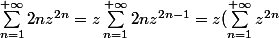'=z. (\dfrac 1{1-z^2})')
 par matheuxendetresse » 02 Mai 2024, 20:37
par matheuxendetresse » 02 Mai 2024, 20:37
Rebonjour,
Oui vous avez raison, ça semble plus rapide, surtout ça donne des séries "usuelles".
Je vous remercie!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
