Eléments d'ordre d dans un groupe cyclique

[ludovic44]

Bonjour,

Je n'arrive pas à me convaincre d'une démonstration.
Soit (G , .) un groupe cyclique d'ordre n et a un générateur de G.

Je souhaite donc prouver que si d divise n, il y a exactement éléments d'ordre d(indicatrice d'Euler).
Je connais déjà le résultat suivant: l'ordre de est

Voici comment la preuve se déroule:

Puisque d divise n, il existe tel que .

On a:



Or, il existe un entier tel que (***)


Ainsi:

C'est donc la phase (***) qui me pose problème. Elle se situe au milieu de deux équivalences. Je comprends que si on suppose que , alors q divise k, d'où l'existence du k'. Mais la réciproque me semble fausse: si , en quoi cela montre que qk' vaut k ? Je n'arrive pas bien à comprendre la structure de la preuve, la phrase au milieu des équivalences me semble bancale...


Je vous remercie d'avance pour vos éclairages.

[Ben314]

C'est le problème des trucs rédigés en Français.
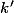
Ce qui est effectivement vrai, c'est que pour un certain entier et là, il n'y a que implication. Mais par contre, ça signifie que où, cette fois, c'est clairement une équivalence. Et on poursuit évidement en écrivant que

Donc la preuve est parfaitement correcte modulo d'interpréter le "Or" de la phrase du milieux correctement.

Et ce type de résultat arch basiques sur les groupes, je t'inciterais plus que fortement à les chercher par toi même du fait que :
- D'avoir cherché soit-même la preuve permet de bien plus facilement mémoriser le résultat.
- Ça fait un très bon début d'entrainement poue se familiariser avec le B-A-BA des preuves concernant le concept en question.
Bref, ce sont certes des "résultat de cours" qu'on pourra utiliser sans les redémontrer, mais ce sont aussi de très très bons exercices "de base" pour se familiariser avec la notion avant d'attaquer les exercices eux-mêmes (et c'est la même chose pour tout les théorème de cours dont la preuve fait moins de 10 lignes)

[ludovic44]

D'accord, merci pour votre réponse, c'est très clair à présent ! Je vais essayer de tenir compte de vos conseils mais parfois, le temps manque hélas !
Bon weekend