Partie non fermé dans R
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par matheuxendetresse » 25 Fév 2024, 12:06
par matheuxendetresse » 25 Fév 2024, 12:06
Salut,
J'ai cette question:
Soient
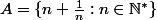
et
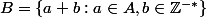
deux parties de l'espace euclidien

La question c'était de démontrer que

est dans l'ensemble d'adhérence de

, et en déduire que

n'est pas fermé.
J'ai bien
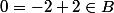
, il est alors dans l'adhérence, et que

est dense dans

sans que les irrationnels soient dedans, alors il est pas fermé.
Mais est-ce que l'on peut le déduire du fait que

est adhérent à

comme propose la question?
Merci!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Fév 2024, 13:49
par Ben314 » 25 Fév 2024, 13:49
Ça m'étonnerais fort que
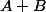
soit dense dans

.
Tu peut me donner, par exemple un point de
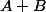
qui appartienne à l'intervalle

?
Sinon, a mon avis, il y a une faute de frappe sur la définition de

qui devrait être
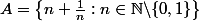
de façon à ce que 2 ne soit pas dans

(et donc que 0 ne soit pas dans
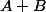
).
Les questions naturelles étant alors de montrer que

et

sont des parties fermées de

, mais pas
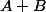
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par matheuxendetresse » 25 Fév 2024, 14:02
par matheuxendetresse » 25 Fév 2024, 14:02
Ben314 a écrit:Ça m'étonnerais fort que
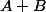
soit dense dans

.
Tu peut me donner, par exemple un point de
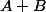
qui appartienne à l'intervalle

?
Ah oui! pardon!
Oui, moi aussi je me suis dit que y a une erreur, car ça donne l'indication que

est dans l'adhérence et pas dans l'ensemble, ce qui est faux.
Du coup, ce que j'ai fait, c'est que j'ai pris
+n+\frac{1}{n})=(2+\frac{1}{n}) \in A+B)
pour

entier naturel strictement positif, et du coup une suite dans
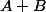
définie comme:
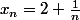
qui converge vers

, et alors ce n'est pas un fermé.
Mercii
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
soit dense dans
.
qui appartienne à l'intervalle
?