Exo sur PGCD ( problèmes )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:02
par Toti08 » 04 Jan 2007, 21:02
Salut, j'ai un exo à faire sur le PGCD et j'ai quelques soucis.
Ils me demandent de calculer le PGCD de A= 2^(n+2) - 2^n
et B= 3^(n+2) - 3^n ( n entier naturel ).
Je n'arrive pas a enlever les n. Mais je me suis demandé s'il ne fallait pas prendre les valeurs maximales que n peut prendre.
Car après simplifications je trouve A= 3*(2^n) et B= (2^3)*(3^n)
Merci d'avance..
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:12
par Toti08 » 04 Jan 2007, 21:12
up... j'ai toujours pas d'idées...
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Jan 2007, 21:19
par BancH » 04 Jan 2007, 21:19
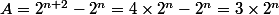
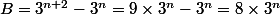

et

sont chacun divisibles par

et par
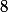
(si
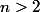
), et comme

et

sont premier entre eux,

et
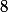
sont leurs seuls diviseurs communs, donc leur PGCD est

-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:22
par Toti08 » 04 Jan 2007, 21:22
ok,... mais il vient d'ou ton n>2 ?
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:24
par Toti08 » 04 Jan 2007, 21:24
je suis pas d'accord ^^
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Jan 2007, 21:26
par BancH » 04 Jan 2007, 21:26
Dans la simplification?
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:26
par Toti08 » 04 Jan 2007, 21:26
je ne comprend pas,..si tu met n>0 alors n peut être égal a 1 et donc A n'est pas divible par 8, ....
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Jan 2007, 21:28
par BancH » 04 Jan 2007, 21:28
Nan ça j'ai modifié, en fait si n=1 le pgcd est 6, si n=2 le pgcd est 12 et si n>2 le pgcd est 24.
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:30
par Toti08 » 04 Jan 2007, 21:30
donc la j'ai compris merci
dernière question, si il demande "le pgcd" dans l'exo, je peux tout de même en donné trois ?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Jan 2007, 21:34
par BancH » 04 Jan 2007, 21:34
Je pense que oui.
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:35
par Toti08 » 04 Jan 2007, 21:35
merci alors pour ton aide.
-
Toti08
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Juin 2006, 18:44
-
 par Toti08 » 04 Jan 2007, 21:45
par Toti08 » 04 Jan 2007, 21:45
tu as dit que 2^n et 3^n étaient premiers entre eux mais faut'il le prouver ?
( avec une recurrence par exemple) ou est ce que c'est admis ?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 04 Jan 2007, 21:55
par BancH » 04 Jan 2007, 21:55
Bah on connaît leur décomposition en nombres premiers, 2^n=2x2x2x2x...x2 et 3^n=3x3x3x3x...x3
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
