Unicité de la solution d'une EDL d'ordre 2

[pringuezz]

Bonjour,

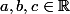
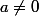
Soient , avec . On considère l'équation différentielle linéaire homogène suivante :

Y-a-t-il un moyen "élémentaire" (c'est-à-dire sans utiliser le théorème de Cauchy-Lipschitz, ni les formules générales donnant les solutions d'une telle équation) de démontrer que si l'on impose une condition initiale et , alors, la solution est unique ?

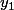
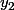
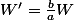
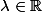
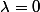
La seule piste que je voie pour l'instant est de montrer "à la main" que si et sont deux solutions, alors, le Wronskien est solution de l'équation , et donc de la forme pour un certain . On en déduit qu'il est soit toujours nul (si ) soit jamais nul. En particulier, si satisfont la même condition initiale, le Wronskien est toujours nul. On peut donc en déduire que pour tout , les vecteurs et sont liés, donc, pour tout , il existe un réel tel que . Mais ensuite, je ne vois comment poursuivre la preuve (et il y a peut-être plus simple...).

Merci d'avance pour vos réponses.

Edit : Si l'on parvient à montrer que la fonction est constante, on a terminé (mais je ne vois pas trop comment on pourrait montrer cela...).

[Ben314]

Salut,
Je ne sais pas trop ce que tu attend comme réponse, mais pour les équations différentielles linéaires à coeff. constant, on peut facilement tout démontrer en "partant de zéro" :
Dans , si on prend on se retrouve avec une équation différentielle en dont les coeff. devant le est donc, si on prend comme une racine (éventuellement complexe) de ce polynôme, on se retrouve avec une équation en de degré un de moins. Et une fois qu'on aura l'expression de , donc de la condition initiale permettra de reconstruire une unique fonction .
En reproduisant le même procédé, au final on va tomber sur une équation de degré zéro (et plus aucune condition initiale), et la solution sera évidement unique ()

[pringuezz]

Merci pour ta réponse.
Oui, je connais cette preuve, mais là, je cherche plutôt (si cela existe) une manière de montrer l'unicité de la solution sans pour autant résoudre l'équation (et sans utiliser des gros résultats comme le théorème de Cauchy-Lipschitz).

[Ben314]

Je vois pas trop en quoi ça pourrait consister une telle preuve : rien que pour celle de degré 1, quelle type de preuve veut tu faire qui n'utilise ni la résolution de l'équation, ni Cauchy-Lipschitz ?