Bonjour,
Le problème est le suivant :
J'ai un cercle de centre C et de rayon r, et un point S en dehors du cercle. J'ai une droite qui passe par C et S, et qui coupe le cercle au point T (celui le plus éloigné de S). Comment connaître les coordonnées de C', milieu du segment TS ? Il y a une contrainte : ne pas calculer les coordonnées de T. Je connais les coordonnées de C, de S, et je connais également le rayon du cercle.
Pour l'instant j'ai essayé d'utiliser les coordonnées barycentriques, mais pour ça il me faudrait quand même les coordonnées de T je pense ? Mais puisque je ne peux pas (je n'ai pas le droit) calculer les coordonnées de T, je ne sais pas du tout comment faire .
D'ailleurs, je n'arrive pas à joindre d'image pour illustrer avec un schéma, désolé.
Est-ce que quelqu'un aurait une idée s'il vous plait ?
Merci d'avance.
Géométrie lycée/licence informatique
3 messages
- Page 1 sur 1
Re: Géométrie lycée/licence informatique
Tu peux calculer les coordonnées de A, milieu de C et S.
Puis considérer un cercle de rayon r/2, de centre A.
Puis considérer un cercle de rayon r/2, de centre A.
Re: Géométrie lycée/licence informatique
Salut,
Je ne comprend pas bien la consigne "ne pas calculer les coordonnées de T".
Si c'est un truc d'informatique et que le programme ne doit pas calculer les coordonnées de T alors il te suffit de les calculer sur une feuille de papier, d'en déduire celles de C' puis de mettre directement dans le programme ce que tu as trouvé pour C' :
\overrightarrow {SC}\ \Rightarrow\ C'\!=\!S+\frac{1}{2}\big(1\!+\!\frac{r}{SC}\big)\overrightarrow {SC})
Que tu peut, si tu préfère, écrire en terme de barycentre :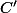 est le barycentre de
est le barycentre de  et
et  affectés des coefficients
affectés des coefficients ) et
et ) .
.
Où le seul truc un peu chiant à calculer, c'est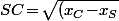^2+(y_C\!-\!y_S)^2})
Je ne comprend pas bien la consigne "ne pas calculer les coordonnées de T".
Si c'est un truc d'informatique et que le programme ne doit pas calculer les coordonnées de T alors il te suffit de les calculer sur une feuille de papier, d'en déduire celles de C' puis de mettre directement dans le programme ce que tu as trouvé pour C' :
Que tu peut, si tu préfère, écrire en terme de barycentre :
Où le seul truc un peu chiant à calculer, c'est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
