Bonjour,
La méthode de factorisation d'Euler permet de factoriser un nombre n lorsqu'il est une somme de deux carrés de deux manières différentes, c'est à dire lorsque n = a² + b² = c² + d².
J'ai déniché une autre méthode (ne me demandez pas d'où ça vient) qui semble faire la même chose :
Soit n = a² + b² = c² + d² (par commutativité on les ordonne pour que a > c > d > b)
On calcule p1, p2, k1, k2 comme ceci :
p1 = ac + bd
p2 = ac - bd
k1 = PGCD(a + d, c - b) * PGCD(a - d, c + b)
k2 = PGCD(a + d, c + b) * PGCD(a - d, c - b)
Si k1 et k2 sont tous deux pairs, on les divise par deux.
Les facteurs x et y de n sont alors égaux à p1 / k1 et p2 / k2
Par exemple, pour n = 1961 = 44² + 5² = 40² + 19²
a = 44
b = 5
c = 40
d = 19
a + d = 44 + 19 = 63
c - b = 40 - 5 = 35
a - d = 44 - 19 = 25
c + b = 40 + 5 = 45
p1 = ac + bd = 1760 + 95 = 1855
p2 = ac - bd = 1760 - 95 = 1665
k1 = PGCD(a + d, c - b) * PGCD(a - d, c + b) = 7 * 5 = 35
k2 = PGCD(a + d, c + b) * PGCD(a - d, c - b) = 9 * 5 = 45
k1 et k2 sont impairs, donc on les laisse tels quels
Donc :
x = p1 / k1 = 1855 / 35 = 53
y = p2 / k2 = 1665 / 45 = 37
Cette méthode semble totalement équivalente à la méthode d'Euler, notamment elle trouve les mêmes facteurs lorsqu'il y en a plus que deux. Mais par contre je n'ai pas la démonstration, et je n'ai pas réussi à en trouver une. Elle ne doit pas être bien plus compliquée que celle de la méthode d'Euler, et vu la forme de p1 et p2 je soupçonne fortement de faire intervenir l'identité de Diophante, en calculant n² = (a² + b²) (c² + d²). Mais après je cale.
* Savez-vous d'où vient cette méthode ?
* Est-ce qu'elle marche dans tous les cas ? Moi je n'ai pas trouvé de contre exemple.
* Saurez-vous trouver une démonstration ?
Variante de la méthode de factorisation d'Euler
7 messages
- Page 1 sur 1
Re: Variante de la méthode de factorisation d'Euler
Sal
Ça l'air "presque" bon, mais pas tout à fait : tu ne divise visiblement pas exactement par ce qu'il faut et ton est parfois un diviseur de
est parfois un diviseur de  et pas
et pas  lui même (ou alors j'ai mal compris ton truc . . .)
lui même (ou alors j'ai mal compris ton truc . . .)
n = 260 = 16² + 2² = 14² + 8²
p1 = 16x14+2x8 = 240
p2 = 16x14-2x8 = 208
k1 = PGCD(16+8,14-2)xPGCD(16-8,14+2) = 12x8 = 96 ---- divisé par 2 ----> 48
k2 = PGCD(16+8,14+2)xPGCD(16-8,14-2) = 8x4 = 32 ---- divisé par 2 ----> 16
donc p1/k1 = 5 et p2/k2 = 13 dont le produit fait 65 et pas 260 (4 fois trop petit)
(Et avec 585, le produit est 9 fois trop petit ; avec 1040 il est 16 fois trop petit . . .)
Je n'ai pas cherché particulièrement à regarder dans quels cas ça ne marche pas, mais il me semble possible que ça fonctionne lorsque l'on suppose en plus que a,b,c,d sont globalement premiers entre eux.
Ça l'air "presque" bon, mais pas tout à fait : tu ne divise visiblement pas exactement par ce qu'il faut et ton
n = 260 = 16² + 2² = 14² + 8²
p1 = 16x14+2x8 = 240
p2 = 16x14-2x8 = 208
k1 = PGCD(16+8,14-2)xPGCD(16-8,14+2) = 12x8 = 96 ---- divisé par 2 ----> 48
k2 = PGCD(16+8,14+2)xPGCD(16-8,14-2) = 8x4 = 32 ---- divisé par 2 ----> 16
donc p1/k1 = 5 et p2/k2 = 13 dont le produit fait 65 et pas 260 (4 fois trop petit)
(Et avec 585, le produit est 9 fois trop petit ; avec 1040 il est 16 fois trop petit . . .)
Je n'ai pas cherché particulièrement à regarder dans quels cas ça ne marche pas, mais il me semble possible que ça fonctionne lorsque l'on suppose en plus que a,b,c,d sont globalement premiers entre eux.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Variante de la méthode de factorisation d'Euler
Effectivement.
Ce n'est donc pas une variante, c'est une autre méthode. Elle donne bien des diviseurs de n, mais différents de la méthode d'Euler. Intéressant...
Ce n'est donc pas une variante, c'est une autre méthode. Elle donne bien des diviseurs de n, mais différents de la méthode d'Euler. Intéressant...
Re: Variante de la méthode de factorisation d'Euler
Après plusieurs tests, je pense que la méthode ne détecte que les facteurs impairs de la forme 4k + 1. Tous les contre-exemples sont pairs ou multiples d'un nombre de la forme 4k+3 (3, 7, 11, ...) :
260 = 13 x 5 x 2 x 2 (les deux facteurs 2 ne sont pas trouvés)
1040 = 13 x 5 x 2 x 2 x 2 x 2 (même chose, les quatre 2 ne sont pas trouvés)
585 = 13 x 5 x 3 x 3 (les deux 3 ne sont pas trouvés)
3185 = 13 x 5 x 7 x 7 (les deux 7 ne sont pas trouvés)
etc...
Et c'est pour ça que je n'ai pas trouvé de contre-exemple, moi je m'étais limité aux produits de nombres premiers impairs de la forme 4k+1, pour être sûr de trouver une somme de carrés. C'était une condition suffisante, mais pas nécessaire : un nombre pair peut être une somme de carrés, et une puissance paire d'un nombre impair (3² par exemple) peut aussi être de la forme 4k + 1 (donc somme de carrés).
260 = 13 x 5 x 2 x 2 (les deux facteurs 2 ne sont pas trouvés)
1040 = 13 x 5 x 2 x 2 x 2 x 2 (même chose, les quatre 2 ne sont pas trouvés)
585 = 13 x 5 x 3 x 3 (les deux 3 ne sont pas trouvés)
3185 = 13 x 5 x 7 x 7 (les deux 7 ne sont pas trouvés)
etc...
Et c'est pour ça que je n'ai pas trouvé de contre-exemple, moi je m'étais limité aux produits de nombres premiers impairs de la forme 4k+1, pour être sûr de trouver une somme de carrés. C'était une condition suffisante, mais pas nécessaire : un nombre pair peut être une somme de carrés, et une puissance paire d'un nombre impair (3² par exemple) peut aussi être de la forme 4k + 1 (donc somme de carrés).
Re: Variante de la méthode de factorisation d'Euler
Dans tout les cas, ton hypothèse  implique directement que
implique directement que (ac\!-\!bd)\!=\!n(c^2\!-\!b^2))
Donc si on cherche des conditions sur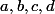 pour que ton truc marche, c'est facile : ça marche ssi le produit des 4
pour que ton truc marche, c'est facile : ça marche ssi le produit des 4  constituant
constituant 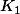 et
et 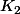 est en fait égal à
est en fait égal à ) ce qui, sauf erreur revient à dire qu'on doit avoir
ce qui, sauf erreur revient à dire qu'on doit avoir \!\times\!\mbox{pgcd}(a\!-\!d,c\!-\!b)\!=\!c\!-\!b)
Donc si on cherche des conditions sur
Modifié en dernier par Ben314 le 08 Jan 2024, 01:31, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Variante de la méthode de factorisation d'Euler
Merci pour ces éléments de réflexion.
Je suis d'accord jusqu'à la dernière égalité pgcd(a + d, c - b) * pgcd(a + d, c - b) = c - b mais je pense que c'est juste une erreur de signe. On aurait pu ajouter pgcd(a + d, c + b) * pgcd(a - d, c + b) = c + b
Par contre, j'ai un peu de mal à suivre le raisonnement. J'ai l'impression (mais peut-être que j'ai mal compris) que c'est un raisonnement circulaire : "Ça marche si et seulement si ça marche". Oui, ça marche ssi le produit des pgcd est égal à c - b, mais le fait est que dans la plupart des cas c'est vrai, et même dans tous les cas simples que j'ai testé (n = produit de deux nombres impairs de la forme 4k + 1).
Mais décomposé comme ceci (et merci encore pour cette piste), je pense qu'on doit pouvoir avoir le même type de raisonnement que pour la factorisation d'Euler, avec les variables h, k, l et m
Je suis d'accord jusqu'à la dernière égalité pgcd(a + d, c - b) * pgcd(a + d, c - b) = c - b mais je pense que c'est juste une erreur de signe. On aurait pu ajouter pgcd(a + d, c + b) * pgcd(a - d, c + b) = c + b
Par contre, j'ai un peu de mal à suivre le raisonnement. J'ai l'impression (mais peut-être que j'ai mal compris) que c'est un raisonnement circulaire : "Ça marche si et seulement si ça marche". Oui, ça marche ssi le produit des pgcd est égal à c - b, mais le fait est que dans la plupart des cas c'est vrai, et même dans tous les cas simples que j'ai testé (n = produit de deux nombres impairs de la forme 4k + 1).
Mais décomposé comme ceci (et merci encore pour cette piste), je pense qu'on doit pouvoir avoir le même type de raisonnement que pour la factorisation d'Euler, avec les variables h, k, l et m
Re: Variante de la méthode de factorisation d'Euler
Oui, j'ai fait un copié-collé sur les deux pgcd sans les changer mais je viens de rectifier,donc ça ne se voit plus.
Sinon, j'ai un peu grattouillé pour voir s'il y avait une condition plus sympathique pour exprimer un truc du style pgcd(A,C)xpgcd(B,C)=C, mais j'ai rien trouvé de bien concluant et j'ai pas vraiment regardé pourquoi cette condition est "souvent" vérifiée dans le contexte présent.
Et en plus, je pense que ça serait sans doute mieux de chercher, comme tu à commencé à le faire, plutôt des conditions sur les facteurs premiers de N plutôt que sur a,b,c,d (au fond, ça revient à peu prés au même, mais je pense que les conditions sur les facteurs de N risque de s'énoncer plus simplement).
Sinon, j'ai un peu grattouillé pour voir s'il y avait une condition plus sympathique pour exprimer un truc du style pgcd(A,C)xpgcd(B,C)=C, mais j'ai rien trouvé de bien concluant et j'ai pas vraiment regardé pourquoi cette condition est "souvent" vérifiée dans le contexte présent.
Et en plus, je pense que ça serait sans doute mieux de chercher, comme tu à commencé à le faire, plutôt des conditions sur les facteurs premiers de N plutôt que sur a,b,c,d (au fond, ça revient à peu prés au même, mais je pense que les conditions sur les facteurs de N risque de s'énoncer plus simplement).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
