Suite récurrente

[Marcet003]

Bonjour,

Je n'arrive pas à conclure à la convergence de cette suite à l'aide du thm. de la convergence monotone.

avec

En fait, j'ai étudier le rapport pour chercher une condition de décroissance. En l'occurence, je trouve que avec 7/3 une approximation assez proche de la racine positive du polynome en obtenu avec la condition de décroissance. Puis j'essaye de montrer par recurrence que cette condition est satisfaite pour tout n, mais je n'y arrive pas. Je n'ai pas envie de prendre la condition sur avec directement la racine.

Avez vous une solution s'il vous plait ?

Merci beaucoup !!

[phyelec]

Bonjour,

Dans un premier temps vous pouvez dire que si une limite existe l elle vérifie :

[phyelec]

vous étudiez la courbe :

[Marcet003]

Merci. Je crois que j'ai pu trouver finalement.

Juste une petite question.
La fct. f(x) en question est croissante. Donc ma suite est décroissante. Mais je sais pas comment le justifier .

Et après je montre qu'elle est bornée inférieurement par 2 par exemple.

[tournesol]

C'est facile:
Les limites de f(x) en 0 et en +infini montrent que
donc
Supposons alors
donc

[Marcet003]

D'accord. Merci du truc.
Mais ce qui m'étonne, c'est de ne pas avoir réussi à determiner la convergence (monotonie notamment) de la suite avec les rapports ou bien ?

Donc si je comprends bien, il y a des cas où ces rapports ne suffisent pas et où il faut passer par l'étude de la fct. de récursion qui définit la suite ?
Est-ce qu'il vaut mieux toujours commencer par étudier la fct. de recursion ou déjà regarder les rapports ?

[tournesol]

La fonction de récursion.

[Marcet003]

D'accord. Merci bcp. bcp !!

[Ben314]

Salut,
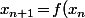Sinon, un truc général qui peut à la limite servir, c'est que si on a une suite définie par une relation de la forme pour tout où une fonction croissante alors la suite est monotone, plus précisément croissante si et décroissante si .
Et la preuve est immédiate vu que la croissance de signifie que, si on a par exemple alors c'est à dire et on conclue par récurrence. (et évidement idem si ).

Faire gaffe par contre à ne pas apprendre le truc de travers (i.e. de dire "f croissante => (xn) croissante" vu que c'est faux) et noter aussi que si f est décroissante, le même raisonnement montre que (xn) ne peut pas être monotone (ou alors elle est constante) vu qu'en fait, une fois sur deux ça va augmenter et une fois sur deux ça va diminuer. Dans ce cas (f décroissante), on peut éventuellement étudier la suite des termes pairs et celle des termes impairs vu que la composée g=fof est une fonction croissante.

[Marcet003]

Excellent, merci. Je crois que je suis incollable maintenant.