Égalité entre 2 intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jean159753
- Messages: 5
- Enregistré le: 16 Juil 2020, 22:47
-
 par jean159753 » 11 Déc 2023, 20:21
par jean159753 » 11 Déc 2023, 20:21
Bonjour,
J'aimerais prouver la relation
 (x+ 2/\alpha -1) (x+2/\alpha)}} = \int_0^1 dx \frac{1}{\sqrt{1-x^2}}\frac{1}{\sqrt{1-(\frac{\alpha}{2})^2(1-x^2)}})
pour

.
J'ai essayé le changement de variable

, ce qui donne après transformation pour la première intégrale

À partir de là je suis bloqué, si vous avez une astuce je suis preneur.
Modifié en dernier par
jean159753 le 12 Déc 2023, 11:21, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2023, 20:47
par Ben314 » 11 Déc 2023, 20:47
Salut,
Tu es sûr de ton résultat ?
Quand on trace les fonction qu'il y a sous les radicaux de tes deux intégrales avec géogébra :
https://www.geogebra.org/classic/npbspszeOn constate qu'une des deux est entièrement en dessous de l'autre lorsque alpha=2 . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jean159753
- Messages: 5
- Enregistré le: 16 Juil 2020, 22:47
-
 par jean159753 » 11 Déc 2023, 20:59
par jean159753 » 11 Déc 2023, 20:59
Oui je suis sûr du résultat

Par contre le résultat n'est correct que dans l'intervalle

.
Edit : même si l'une des fonctions est en dessous de l'autre sur presque tout l'intervalle, l'intégrale passe par 1 ou 2 racines du polynômes (x=1 pour g ou x=0 et x=1 pour f).
-
jean159753
- Messages: 5
- Enregistré le: 16 Juil 2020, 22:47
-
 par jean159753 » 12 Déc 2023, 17:44
par jean159753 » 12 Déc 2023, 17:44
J'ai trouvé. Pour prouver l'égalité j'ai commencé par faire un premier changement de variable

puis un autre

.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 12 Déc 2023, 18:38
par Pisigma » 12 Déc 2023, 18:38
Bonjour,
je n'ai pas eu le courage d'essayer tes changements de variables, mais je suis quand même curieux de voir le
détail de ton calcul car si je prends
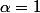
et fait calculer les deux intégrales de départ,
par
Wolfram,on trouve bien la même chose (
)
mais
Wolfram passe par des intégrales elliptiques!!
-
jean159753
- Messages: 5
- Enregistré le: 16 Juil 2020, 22:47
-
 par jean159753 » 12 Déc 2023, 18:49
par jean159753 » 12 Déc 2023, 18:49
Bonjour,
Oui le résultat est une intégrale elliptique
 (x+ 2/\alpha -1) (x+2/\alpha)}} = K(\alpha^2/4).)
Pour le prouver j'ai fait le changement de variable

Puis on prouve que
)
est équivalent à la deuxième intégrale de mon premier message (qu'on peut écrire en fonction de K :
) \frac{1}{\sqrt{4-\alpha^2}})
).
Edit : Le calcul est assez long mais je peux donner
 }{2 (x -1 + 2/\alpha)^{3/2} \sqrt{2x/\alpha}})
. De plus on remarque que le changement de variable ne modifie pas les bornes. Ensuite il faut inverse la relation entre x et x' et on voit qu'on obtient une intégrale elliptique du premier type.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 12 Déc 2023, 19:00
par Pisigma » 12 Déc 2023, 19:00
perso il y a un certain temps, je dirais même un temps certain, que je n'ai plus manipulé ce type d'intégrale, bravo!
je suppose que tu "fais" des maths de haut niveau
-
jean159753
- Messages: 5
- Enregistré le: 16 Juil 2020, 22:47
-
 par jean159753 » 12 Déc 2023, 19:09
par jean159753 » 12 Déc 2023, 19:09
Plutôt de la physique

Je suis tombé sur cette intégrale en travaillant sur un problème.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2023, 03:06
par Ben314 » 13 Déc 2023, 03:06
Chapeau. . .
J'ai un peu cherché, mais sans rien trouver, mais il faut dire que j'ai pas pensé à passer par un truc du style de ton "intermédiaire" où le polynôme sous la racine n'est plus que de degré 3.
J'y connait quasi que dalle aux intégrales elliptiques, mais je pensait (bêtement...) que celle de type ??? (degré 4 sous la racine en bas) restaient sous cette forme par tout changement de variable homographique : ERREUR !!!
Mais c'est une bonne chose, ça a un peu dérouillé ma vieille cervelle qui en a bien besoin . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités