Bonjour, j'esperes que vous allez bien.
J'aimerais comprendre une petite nuance dans mon cours de geo diff. Dans la definition de mon cours d'une application differentiable entre 2 variétés M et N, on a le suivant:
f: M->N est de classe Cp si pour tout a dans M, il existe une carte (U, phi) de M en a, et une carte (V, psi) de N en f(a) telles que psi rond f rond phi^-1 soit de classes Cp.
mais dans plusieurs exercices, on dit que cela n'est pas suffisant, il faut aussi montrer que phi rond f rond psi^-1 soit de meme de classe Cp. Ma question, est il suffisant en general de montre une des deux? ou bien faut-il les 2 applications pour que f soit de classe Cp?
Geometrie differentielle, variétés
6 messages
- Page 1 sur 1
Re: Geometrie differentielle, variétés
Salut,
Je sais pas si "c'est suffisant", mais par contre, ce que je vois, ben c'est que c'est passablement incohérent . . .
Si tu as des applications avec
avec  et
et  bijectives alors,
bijectives alors,
- Autant je vois parfaitement bien comment les composer "de gauche à droite", (i.e. )
)
- Autant le , de la fin de ta prose, je voudrais bien que tu m'explique à quoi il correspond . . .
, de la fin de ta prose, je voudrais bien que tu m'explique à quoi il correspond . . .
On t'a jamais expliqué que, pour pouvoir composer des fonctions, il fallait un minimum de cohérences entre les ensemble de départ et d'arrivé des fonctions en question ?
Je sais pas si "c'est suffisant", mais par contre, ce que je vois, ben c'est que c'est passablement incohérent . . .
Si tu as des applications
- Autant je vois parfaitement bien comment les composer "de gauche à droite", (i.e.
- Autant le
On t'a jamais expliqué que, pour pouvoir composer des fonctions, il fallait un minimum de cohérences entre les ensemble de départ et d'arrivé des fonctions en question ?
Modifié en dernier par Ben314 le 25 Nov 2023, 11:35, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Geometrie differentielle, variétés
ma question suppose que cette coherance existe, mais j'ai pas noté cela
Re: Geometrie differentielle, variétés
A mon avis tu as lu complètement de travers et la composition "dans l'autre sens", c'est pas pour montrer que  est différentiable, mais pour montrer que c'est un difféomorphisme, c'est à dire une bijection différentiable et dont la bijection réciproque est elle aussi différentiable.
est différentiable, mais pour montrer que c'est un difféomorphisme, c'est à dire une bijection différentiable et dont la bijection réciproque est elle aussi différentiable.
Et dans ce cas là, effectivement, un fois démontré que est bijective, ce qu'il faut montrer (par définition) pour montrer que la réciproque est différentiable, c'est que
est bijective, ce qu'il faut montrer (par définition) pour montrer que la réciproque est différentiable, c'est que  est différentiable.
est différentiable.
Et dans ce cas là, effectivement, un fois démontré que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Geometrie differentielle, variétés
P.S. Et je te demande pas de te rappeler si cette cohérence de composée était avérée ou pas dans ce que tu as lu, je te demande d'utiliser ta cervelle et de comprendre ce que ça signifierais qu'on ait le droit de composer les fonctions dans cet ordre.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Geometrie differentielle, variétés
Bonjour,
Ben314 a fait une coquille, la réciproque de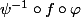 , c'est bien sûr
, c'est bien sûr 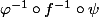 .
.
Ben314 a fait une coquille, la réciproque de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
