DM Math Polynome

[23rdspring]

Bonjour,
Cela ne semble pas si difficile pas je bloque quand même sur cette question. Pourrait on m'aider s'il vout plait.

L'énoncé:

Un polynome defini pour tout nombre complexe z, P(z)=z^4-2z+λ, avec λ un nombre réel.

Montrer que si o est une racine complexe de P alors son conjugué o barre.

Merci

[Pisigma]

Bonjour,

Montrer que si o est une racine complexe de P alors son conjugué o barre ????.(il manque un bout)

[catamat]

Bonjour
Utilise les propriétés du conjugué pour transformer :



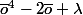
sachant que est réel donc égal à son conjugué.

[23rdspring]

Bonjour,

Montrer que si o est une racine complexe de P alors son conjugué o barre ????.(il manque un bout)

Le reste c'est : "o barre est une racine de P"

[23rdspring]

Bonjour
Utilise les propriétés du conjugué pour transformer :



sachant que est réel donc égal à son conjugué.

Bonjour,

J'ai essayé et j'ai écrit :













Merci