Transfinis

[axeltur]

Bonjour, j'ai regardé cette video sur les nombres transfinis :

https://www.youtube.com/watch?v=kl34kGu ... 0t&index=8

je ne comprends pas pourquoi omega puissance omega est denombrable, intuitivement j'ai l'impression que ca corresponderait a l'infini puissance l'infini (infini x infini x infini x...), or 2 puissance l'infini est indenombrable (voir infini sur wikipedia, paragraphe nommé: "Le cardinal de l'ensemble des parties d'Aleph 0" (ctrl+f permet de surligner le texte voulu) )
donc ca devrait au moins etre egal a 2 puissance l'infini.
Des précisions pour que je comprenne ?

[hdci]

Bonjour,

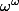est l'ensemble de tous les ordinaux strictement inférieur à 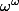: or si alors il existe un certain entier tel que

On peut donc écrire



qui est une réunion dénombrable d'ordinaux dénombrables. Donc dénombrable.

On peut aussi voir les choses ainsi :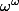 est équipotent (en bijection avec) l'ensemble des suites d'entiers à support fini, qui est un ensemble dénombrable

[Ben314]

Salut,
Les ordinaux, c'est la classe des ensembles bien ordonnés or, autant on peut mettre une relation de bon ordre sur un produit fini d'ensembles bien ordonnés (à savoir l'ordre lexicographique) autant ce n'est plus possible pour un produit infini d'ensembles bien ordonné.
Donc, sur les ensembles bien ordonnés, on a défini une notion d'exponentiation qui n'est pas le même que celle pour les ensembles quelconques :
- Pour un ensemble quelconque la notation correspond à l'ensemble de toutes les applications de dans , c'est à dire l'ensemble de toutes les suites où et, on peut montrer que, dés que le cardial de de est , l'ensemble est non dénombrable.
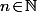- Par contre, dans le contexte des ordinaux (i.e. des ensembles bien ordonnés), cette même notation désigne la réunion des pour (car 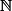est un ordinal limite : regarde la définition générale sur la page de Wiki si tu veut) c'est à dire en fait l'ensemble de des suites telles que (min. de ) pour tout suffisamment grand. Et avec cette définition là, on vérifie facilement que est au plus dénombrable lorsque est au plus dénombrable.

Bref, le problème c'est que la même notation désigne deux choses différentes en fonction du contexte et, à mon avis, ça explique en grande partie que l'on note de façon différente ou le même ensemble selon qu'on le regarde comme un ensemble "classique" ou bien un comme un ordinal : .

[axeltur]

qui est une réunion dénombrable d'ordinaux dénombrables. Donc dénombrable.

merci pour ta reponse, je viens de regarder sur wikipedia, la page ensemble denombrable et il y est dit que ca repose sur l'axiome du choix, qui n'est pas prouvé mais supposé vrais... Cette preuve ne me convient pas, en connais-tu une autre ?

[hdci]

On a besoin de l'axiome du choix lorsque l'on ne peut pas "expliciter" les éléments : si les ensembles sont dénombrables, alors pour chaque il existe "une" bijection et c'est ce "une" qui nécessite l'axiome du choix.

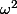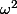Mais ici on est dans des ensembles bien ordonnés et l'axiome du choix n'est pas requis. en effet, l'aspect bien ordonné nous permet d'expliciter les bijections par récurrence : en partant de la première triviale de , on peut expliciter une bijection de dans en remarquant que est équipotent à et on sait construire (identifier) une bijection de sur .
Alors est équipotent à et par composition de la bijection de et celle de on obtient une bijection de

On voit ici la construction par récurrence : si on a identifié une bijection de alors on sait identifier une bijection de

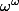Ce qui fait qu'on dispose maintenant d'une suite où est la bijection, et de là on sait construire une bijection de la réunion des (qui est exactement ) sur .

Voici une description de cette construction : dans un plan, quadrant positif, tracer les demi-droites verticales correspondant aux abscisses entières, et numéroter les points à ordonnées entières de ces droites en diagonale : 0 correspond à (0;0) ; 1 correspond à (0;1) ; 2 correspond à (1;0) ; 3 correspond à (0;2) ; 4 correspond à (1;1) , etc.. Chaque droite correspond à un , les ordonnées correspondent à l'image par la bijection dans et la numérotation en diagonale permet de construire (ici visuellement) une surjection (puisque les ne sont évidemment pas disjoints deux à deux, mais inclus l'un dans l'autre...) de dans .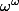
Comme les ensembles sont bien ordonnés on peut en déduire une injection de (en prenant pour image réciproque le "plus petit des antécédents" et on a une injection d'un ensemble dans un sous-ensemble, le théorème de Cantor Bernstein permet d'en déduire qu'il y a une bijection entre ces deux ensembles.


C'est un peu long et laborieux, il existe peut-être "plus court", mais c'est ce qui me vient à l'esprit juste là dans l'instant...

[axeltur]

Mais ici on est dans des ensembles bien ordonnés et l'axiome du choix n'est pas requis. en effet, l'aspect bien ordonné nous permet d'expliciter les bijections par récurrence.

j'ai deja vu des reccurences qui demontres que pour tout n fini, telle propriete est vrais,

mais je n'ai jamais vu de réccurence dire que la propriete est vrais a l'infini aussi, peut-tu m'expliquer comment tu integre l'infini ?

[Ben314]

L'application qui, à toute suite d'entiers naturels dont les termes sont tous nuls à partir d'un certain rang, associe l'entier naturel non nul (où est le -ième nombre premier) est évidement bijective et n'utilise bien évidement pas l'axiome du choix.

[hdci]

j'ai deja vu des reccurences qui demontres que pour tout n fini, telle propriete est vrais,

mais je n'ai jamais vu de réccurence dire que la propriete est vrais a l'infini aussi, peut-tu m'expliquer comment tu integre l'infini ?

Je ne suis pas sûr de bien comprendre ta question : ici je n'utilise pas la récurrence pour démontrer qu'une propriété est vraie, mais j'utilise une définition par récurrence pour définir formellement un ensemble.

Le théorème sous-jacent est le suivant :
Etant donné un ensemble non vide , un élément et une application , alors il existe une unique fonction telle que et

Et par conséquent, est un ensemble défini par récurrence (ou par "itération" si on veut éviter de confondre avec le "raisonnement par récurrence").
(C'est exactement le même principe qui permet de définir une suite par une relation de récurrence : point de départ et mécanisme pour passer au suivant, et cela donne l'existence et l'unicité de la suite, tant que le mécanisme est bien une application et non une simple fonction).

Ainsi, dans le contexte de ce théorème et en reprenant mon précédent propos, l'ensemble est la réunion des ensembles des bijections de (l'ensemble existe car l'ensemble des bijections de est une partie d'un certain produit cartésien, partie non vide car est dénombrable, et la réunion est un axiome de la théorie des ensembles) et la fonction est celle qui à chaque bijection définie sur associe une bijection définie sur qui est bien une application de (tout élément de admet bien une unique image dans par le mécanisme indiqué).

Et le théorème que j'ai cité précédemment, qui ne s'appuie pas sur l'axiome du choix, garantit l'existence de la suite à partir d'une bijection initiale , et c'est cette suite qui permet de construire la bijection sur .

(Le théorème ci-dessus se démontre en considérant le sous-ensemble de toutes les parties de qui vérifient les conditions requises : la partie contient et pour tout élément de la partie, elle contient .
On considère alors l'intersection de toutes ces parties et on démontre que c'eszt bien la fonction recherchée et qu'elle est unique.)

[axeltur]

j'ai deja vu des reccurences qui demontres que pour tout n fini, telle propriete est vrais,

mais je n'ai jamais vu de réccurence dire que la propriete est vrais a l'infini aussi, peut-tu m'expliquer comment tu integre l'infini ?

Je ne suis pas sûr de bien comprendre ta question : ici je n'utilise pas la récurrence pour démontrer qu'une propriété est vraie, mais j'utilise une définition par récurrence pour définir formellement un ensemble.

je pensais que tu faisais une reccurence sur w^n, soit w^n est denombrable alors w^n+1 l'est aussi.
quoi qu'il en soit j'ai l'impression que ca ne répond pas a ma question: qu'en est-il de w^w (ou w^infini) puisque N decrit l'ensemble des entiers mais plus petits que l'infini donc w^w n'est pas pris en compte puisque w (qui correspond a l'infini) n'est pas dans N

[hdci]

Si cela répond bien à la question : j'ai identifié, sans utiliser l'axiome du choix, une bijection de ce qui montre que l'ensemble est bien dénombrable.

Pour aller plus loin : comme je l'ai déjà dit je crois,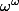 représente l'ensemble des suites d'entiers naturels à support fini (c'est-à-dire, nulle à partir d'un certain rang), et cet ensemble est dénombrable, contrairement à l'ensemble qui représente l'ensemble des suites "tout court" qui lui n'est pas dénombrable, tout comme , ensemble des suites constituées de 0 et de 1, qui est également indénombrable.

Il y a une différence fondamentale dans l'arithmétique des ordinaux et l'arithmétique des cardinaux (entre autres l'addition dans les ordinaux n'est pas commutative alors qu'elle l'est dans les cardinaux...), il te faut revenir aux définitions si tu as des confusions à ce sujet

On peut également le voir ainsi :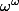 est la limite (la borne supérieure) de la suite . Or cette suite est une suite croissante d'ordinaux dénombrables, et la borne supérieure d'une telle suite est nécessairement dénormbable (c'est en fait la même démonstration). Cela peut surprendre, mais le parallèle est le suivant : si est une suite croissante et finie d'entiers (fnie dans le sens : il n'y a qu'un nombre fini de termes), alors la borne supérieure est forcément fnie : on ne peut pas atteindre l'infini dénombrable à partir d'une séquence finie d'entiers. De la même façon, on ne peut pas atteindre le premier infini indénombrable à partir d'une séquence dénombrable d'ordinaux dénombrables. Et on montre de façon générale qu'on ne peut pas atteindre (le cardinal infini de rang n) à partir d'une suite croissante d'ordinaux de cardinal strictement inférieur à , suite dont le cardinal est inférieur strictement à

[axeltur]

Merci d'avoir essayé de m'expliquer, malheureusement je ne comprends pas, (malgres que j'ai fait 2 années de prépa PC) pour moi une proprieté qui fonctionne sur N ne fonctionne pas forcément sur l'infini, par exemple la propriété suivante:
"n est fini" est clairement fausse quand on prend pour n la valeur de l'infini.
je n'ai pas répondues aux autres commentaires (de ben314) car je les comprends encore moins.

[hdci]

En complément : il faut rappeler la définition de l'exponentiation : pour tout ordinal , on a

• 
• Pour tout ordinal
• Pour tout ordinal limite (ordinal sans prédécesseur),

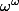Il en découle que l'exposant "ordinal limite" revient à prendre la réunion de tous les ordinaux exposant précédent : ainsi est bien la réunion des pour n entier.

L'ordinal peut aisément être associé aux suites d'entiers nulle à partir du rang (ainsi, correspond à la suite nulle, correspond à la suite dont le terme de rang 0 est un entier quelconque et tous les autres termes sont nuls, 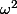correspond à la suite dont les deux premiers termes sont un couple d'entiers quelconques et tous les autres termes sont nuls, etc. ; il n'est pas trop difficile de faire une bijection entre ces ensembles de suite et le correspondant) : ce qui fait que 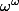est bien l'ensemble de toutes les suites d'entiers qui sont nulles à partir d'un certain rang.

Ce qui est très différent de , ensemble de toutes les suites d'entiers (qui lui est indénombrable).

Attention également à ne pas confondre arithmétique des ordinaux et arithmétique des cardinaux (deux notions différentes : l'addition des ordinaux n'est pas commutative alors qu'elle l'est pour les cardinaux...)

[hdci]

Si tu veux "plus de détail" sur la construction, tu peux consulter mon blog qui comporte quelques documents sur la théorie des ensembles :http://hdci.unblog.fr/theorie-des-ensembles-zfc/

J'ai écrit ces documents il y a quelques années déjà, mais il faut un peu de temps pour s'y plonger...

[axeltur]

Merci, j'ai peut être compris, la dernière valeur de w^w est dénombrable car on peut l'écrire d'une infinité de manière différentes mais l'ensemble w^w est fini car il ne prends on compte qu'une de ces valeurs dénombrables.

[hdci]

L'ensemble n'est pas fini, il est dénombrable, il contient tous les ordinaux qui lui sont strictement inférieur.
Il n'y a pas de "dernière valeur" dans l'ensemble (au sens "plus grand élément"), de la même façon qu'il n'y a pas de "dernier entier naturel" dans .