Continuité, noyau

[Sameraz]

Bonjour chers amis,
Je me trouve bloqué sur une technique utilisée par mon prof pour montrer une equivalence. J'ai bien compris la demarche mais je n'arrive pas a comprendre pourquoi on a fait cela.
La question est:
Soit f une forme linéaire de (E, ||.||)->R . Montrer l'equivalence:
F est continue <=> Ker(f) est fermé.
La premiere implication est triviale.
Pour la deuxieme (<=) , j'ai bien compris la premiere partie:
On a distingué 2 cas, si x est dans Kerf ou non.
Si x est dans Kerf, f(x)=0 et donc |f(x)|<C.||x|| toujours donc f est continue (etant lineaire)
Si x est en dehors du Ker, f(x) est non nulle. Donc sans perte de generalite on a consideré f(x)>0.
De plus, comme Kerf est fermé, E-Kerf est ouvert donc on peut trouver un r>0 tel que B(x,r) est incluse dans E-Kerf. J'ai bien compris jusque la. Ce qui m'echappe c'est la suite:
En supposant que f(x)>0, montrons que pour tout a dans B(x,r), f(a) >0

[hdci]

Bonjour,

La démonstration n'est sûrement pas terminée : qu'est-ce qui te bloque ? Démontrer que ou savoir pourquoi on veut montrer que ? Quelle est la suite de la démonstration ?

Dans l'attente de ta réponse, voici pourquoi :

Avec et sachant que , supposons qu'il existe tel que

On considère le segment reliant et , qui est inclus dans la boule (facile à vérifier avec l'inégalité triangulaire), et qui peut s'exprimer par avec .*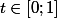
On peut alors voir qu'il existe un tel que , en effet :



et puisque et sont de signes contraires la différence n'est pas nulle et est supérieure à , donc est bien un réel entre 0 et 1.

Ce qui fait que la boule rencontre le noyau ce qui est contradictoire avec la boule hors du noyau.

Il en résulte que dans la boule tous les vecteurs ont une image strictement positive.

[Sameraz]

Bonjour,
Merci pour votre reponse. Votre demarche est exactement une partie de la le suite de la demonstration, mais je voulais savoir pourquoi on cherche a montrer f(a)>0 .
De plus, pourquoi sur le segment joignant a à x il est necessaire que f s'annule? (On ne sait pas que f est continue,on cherche a le montrer)

[hdci]

Pour l'annulation sur le segment 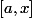: je n'utilise certainement pas la continuité ! J'ai simplement résolu l'équation en t suivante :


Vérifie que la valeur est solution de cette équation, d'une part, et que cette solution est bien comprise entre 0 et 1, d'autre part. Cela montre, continuité ou pas, qu'il existe un vecteur sur le segment dont l'image est nulle.

Pourquoi la démonstration part sur ? Je n'en sais rien, ce n'est pas cette démonstration que je connais ; celle que je connais, par l'absurde, consiste plutôt à construire une suite de vecteurs dans Kerf, qui converge vers x bien que f(x)=0, ce qui contredit l'aspect fermé du noyau
(En substance : si la fonction n'est pas continue, elle ne l'est pas en 0, on construit donc une suite qui converge vers le vecteur nul mais dont les images sont toujours strictement supérieure à un certain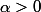 ; ce qui permet de construire une suite convergeant vers le vecteur nul et dont les images sont toujours égale à 1, puis en combinant avec x, une suite qui converge vers x et dont les images sont toujours nulles).

Qu'y a-t-il dans ta trame de démonstration, après ?