Pavage achevé et non achevé

[Arc]

Bonjour, j'espère que vous allez bien.

Dans un problème, on définit ce qu'un pavage et son caractère achevé comme suit : https://ibb.co/6ggjBLT
Ma question est la suivante:
La définition d'un pavage n'est elle pas suffisante pour montrer par récurrence, pout tout entier n, et pour toute famille (An) d'éléments de ce pavage, la propriété;
A0 U ..... U An est un élément de ce pavage ?
et que A0 ∩ ..... ∩ An est un élément de ce pavage ?
dans ce cas, tout pavage serait achevé ?

Merci d'avance.

[GaBuZoMeu]

Bonjour,
As-tu remarqué qu'il s'agit dans la condition d'achèvement d'union (et d'intersection) infinie dénombrable ? Ta récurrence n'arrive qu'à des unions et intersections finies.
Prend par exemple pour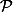 l'ensemble des parties finies d'un ensemble infini . C'est un pavage qui n'est pas achevé.

[Arc]

Bonjour,
Merci beaucoup ! tout s'éclaircit maintenant.
Bonne journée

[GaBuZoMeu]

Avec plaisir.