Base duale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ludovic44
- Membre Naturel
- Messages: 76
- Enregistré le: 12 Juin 2021, 12:22
-
 par ludovic44 » 14 Oct 2023, 06:34
par ludovic44 » 14 Oct 2023, 06:34
Bonjour,
On considère une base
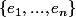
d'un e.v E de dimension n.
On considère les formes linéaires
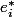
définies par:
=1)
si
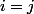
et 0 sinon.
J'ai bien compris pourquoi les
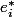
forment une base de
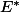
mis à part le fait que je bloque (certainement bêtement) pour prouver que ces applications sont linéaires.
Cela semble à chaque fois admis car trivial dans les différentes sources que j'ai pu lire.
Soit

. On peut écrire
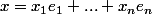
. De même, Soit
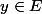
. On peut écrire
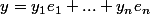
.
=e^*_1((x_1+y_1)e_1+...+(x_n+y_n)e_n))
=???
Je ne vois vraiment pas comment montrer cela !
Merci pour votre aide
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 14 Oct 2023, 10:01
par Kolis » 14 Oct 2023, 10:01
Tu dis que tu as des formes linéaires et tu demandes pourquoi elles le sont ? Ou alors je n'ai pas compris ton problème !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Oct 2023, 10:56
par GaBuZoMeu » 14 Oct 2023, 10:56
Bonjour,
La définition de la base duale te dit que
=x_1)
.
-
ludovic44
- Membre Naturel
- Messages: 76
- Enregistré le: 12 Juin 2021, 12:22
-
 par ludovic44 » 14 Oct 2023, 12:42
par ludovic44 » 14 Oct 2023, 12:42
Bonjour, merci pour vos réponses !
Kolis: je ne suis pas très clair, je voulais dire que je sais que ce sont des formes linéaires mais je n'arrive pas à le prouver !
GaBuMeu: moi j'aimerais partir de la définition des
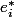
que j'ai donné. Et puisqu'il s'agit de formes linéaires (même si je n'arrive pas à le prouver), alors le fait qu'elles associent à un vecteur

sa
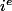
coordonnées est alors une conséquence de cette linéarité non ?
Si
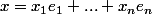
, alors
=x_1e^*_1(e_1)+...+x_ne^*_n(e_n)=x_i)
.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Oct 2023, 12:56
par GaBuZoMeu » 14 Oct 2023, 12:56
Tu sembles oublier un résultat basique d'algèbre linéaire que tu as déjà sûrement vu.
Soit
)
une base de l'espace vectoriel

et soit
)
une famille d'éléments de l'espace vectoriel

. Alors il existe une unique application linéaire
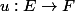
telle que
=a_i)
pour
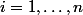
, et cette application linéaire est définie par
=x_1a_1+\cdots+x_na_n)
.
Rappel : une forme linéaire, ce n'est pas autre chose qu'une application linéaire à valeurs dans le corps de base.
-
ludovic44
- Membre Naturel
- Messages: 76
- Enregistré le: 12 Juin 2021, 12:22
-
 par ludovic44 » 14 Oct 2023, 15:25
par ludovic44 » 14 Oct 2023, 15:25
Oui, en effet, je n'avais pas en tête ce résultat ! Je vais creuser, merci

-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 14 Oct 2023, 22:16
par tournesol » 14 Oct 2023, 22:16
Tu veux démontrer que ces formes sont linéaires à partir de leur définition.
Par exemple motrer que
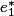
est linéaire.
Si sa définition est:
l'unique forme linéaire telle que
=1)
et pour tout i supérieur à 1 ,
=0)
,
alors il n'y a rien à démontrer puisque
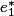
est lineaire par hypothèse.
Si sa définition est la fonction première coordonnée dans la base
)
, c'est à dire
=x_1)
alors on peut montrer la linéarité:
Soient a et b deux réels ,
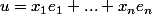
et
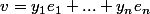
=e_1^*(a(x_1e_1+...+x_ne_n)+b(y_1e_1+...+y_ne_n)))
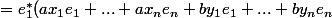=e_1^*((ax_1+by_1)e_1+...+(ax_n+by_n)e_n))
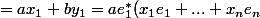+be_1^*(y_1e_1+...+y_ne_n)=ae_1^*(u)+be_1^*(v))
-
ludovic44
- Membre Naturel
- Messages: 76
- Enregistré le: 12 Juin 2021, 12:22
-
 par ludovic44 » 15 Oct 2023, 07:47
par ludovic44 » 15 Oct 2023, 07:47
Merci pour cette réponse détaillée.
Ce que je n'avais pas bien cerné, c'était plutôt avec la première définition. Car lorsqu'on dit, par définition, la forme linéaire telle que
=1)
si i=j et 0 sinon, alors cette définition n'a de sens que si cette forme linéaire existe.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 15 Oct 2023, 08:47
par GaBuZoMeu » 15 Oct 2023, 08:47
orsqu'on dit, par définition, la forme linéaire telle que
=1)
si
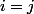
et

sinon, alors cette définition n'a de sens que si cette forme linéaire existe.
Une nouvelle fois, tu devrais bien te rentrer dans la tête qu'on définit une et une seule application linéaire en donnant les images des vecteurs d'une base de l'espace de départ !
-
ludovic44
- Membre Naturel
- Messages: 76
- Enregistré le: 12 Juin 2021, 12:22
-
 par ludovic44 » 15 Oct 2023, 09:58
par ludovic44 » 15 Oct 2023, 09:58
Oui oui, tout à fait, j'ai bien compris à l'aide de ton précédent message. Merci encore

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
