Diagonalisation d'une matrice

[ERRAZKA]

Bonjour tous le monde. J'ai la question suivante concernant la diagonalisation de la matrice suivante:

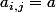si i<j et 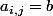si i>j et .

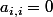Merci d'avance.

[Ben314]

Salut,
As-tu calculé le polynôme caractéristique de la matrice ?
Et tu veut (éventuellement) la diagonaliser sur quel corps ? (et a et b vivent où ?)

EDIT : le polynôme caractéristique est effectivement calculable et on peut trouver les valeur propres.

[ERRAZKA]

Merci Ben, en fait , et on veut déterminer sous quelle condition pourtant sur a et b pour la matrice soit diagonalisable et en trouvant les valeurs propres. J'ai trouvé une proposition s'il n'y a pas d'erreur. Voilà ma proposition

https://drive.google.com/file/d/1q6fuxWtgmLIpD_08HiWrt1fMv7IGUlKc/view?usp=sharing