Explication calcul factorielle ( Maths expertes )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ouâemren
- Messages: 2
- Enregistré le: 23 Sep 2023, 11:32
-
 par Ouâemren » 23 Sep 2023, 11:40
par Ouâemren » 23 Sep 2023, 11:40
Bonjour, nous avons étudié la formule de Pascal en cours notamment la démonstration que j'ai plutôt bien comprise il y a juste un passage de celle-ci que j'ai du mal à saisir, c'est le calcul suivant :
(n-k-1)!(n-k) = (n-k)!
Je ne comprends pas pourquoi le "-1" disparaît si quelqu'un peut me l'expliquer.
Merci d'avance


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Sep 2023, 12:11
par Ben314 » 23 Sep 2023, 12:11
Salut,
Il n'y a évidement rien du tout qui "disparaît". Ta formule dit, par exemple, que
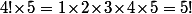
.
De même, pour tout entier naturel non nul

, tu as
!\!\times\!m=m!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Ouâemren
- Messages: 2
- Enregistré le: 23 Sep 2023, 11:32
-
 par Ouâemren » 23 Sep 2023, 14:46
par Ouâemren » 23 Sep 2023, 14:46
Ben314 a écrit:Salut,
Il n'y a évidement rien du tout qui "disparaît". Ta formule dit, par exemple, que
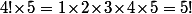
.
De même, pour tout entier naturel non nul

, tu as
!\!\times\!m=m!)
Ok je comprend mieux merci beaucoup
-
mathou13
- Membre Relatif
- Messages: 204
- Enregistré le: 08 Juin 2019, 14:52
-
 par mathou13 » 24 Sep 2023, 17:41
par mathou13 » 24 Sep 2023, 17:41
Bonjour,
(n-1)!*n=n!
Donc (n-k-1)!*(n-k)=(n-k)! En remplaçant n par n-k
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
.
, tu as