Probas, suites

[gaelle3brm]

Bonjour, j'ai un DM de niveau BCPST 2 et je suis bloquée... Pouvez-vous m'aiguiller svp ?

Voici l'énoncé :
Soit c un nombre réel. On donne 12 (Xn+2) - 6 (Xn+1) + Xn = c
1) trouver les suites qui vérifient :
a) quand c=0
b) dans les autres cas, on pourra poser Xn' = Xn - a en choisissant adroitement a.
2)On a une roue divisée en 3 tiers : Z=1, Z=2, et Z=3. On fait tourner la roue et le curseur d'arrête dans la partie 1, 2 ou 3. On note Pn, Qn et Rn la probabilité de faire respectivement 1, 2 ou 3 au lancer n. Après avoir lancé la roue, la probabilité d'obtenir le même numéro au lancer suivant est de 1/2 ; la proba d'obtenir le numero précédent est de 1/6 ; et la proba d'obtenir le numero suivant est de 1/3.
a) Expremier P(n+1), Q(n+1) et R(n+1) en fonction de Pn, Qn et Rn.
b) Donner une relation entre Pn, Qn et Rn
c) Exprimer P(n+1) et Q(n+1) en fonction de Pn et Qn.

Voilà où j'en suis :
1a) c'est une suite recurrente d'ordre 2, avec des racines complexes. J'ai obtenu Xn=(sqrt3/6)^n.[lambda1.cos(-n.pi/6) + lambda2.sin(-n.pi/6).
b) je ne sais pas comment partir... Comment savoir la valeur de a ??

2a) j'ai trouvé ceci mais j'ai peur d'avoir un peu mélangé tous les coefficients...
Pn+1 = 1/2Pn + 1/3Qn + 1/6Rn
Qn+1 = 1/6Pn + 1/2Qn + 1/3Rn
Rn+1 = 1/3Pn + 1/6 Qn + 1/2Rn
b) Pn+1 + Qn+1 + Rn+1 = 1
c) je ne sais pas comment m'y prendre

J'espère que quelqu'un pourra m'éclairer...
Bonne soirée

[GaBuZoMeu]

Bonjour,
As-tu donné exactement l'énoncé de la question 2 ?
Les zones 1,2,3 ne sont pas équiprobables ?
Pour moi la question est incompréhensible telle que tu la formules.

[gaelle3brm]

Ah oui pardon j'ai sauté une ligne en recopiant ! On nous dit aussi :
Après avoir lancé la roue, la probabilité d'obtenir le même numéro au lancer suivant est de 1/2 ; la proba d'obtenir le numero précédent est de 1/6 ; et la proba d'obtenir le numero suivant est de 1/3.

[Ben314]

Salut,
Pour la question 1)b), il suffit de suivre scrupuleusement l'indication, c'est à dire de remplacer par dans la relation de récurrence puis d'en déduire la valeur à prendre pour de façon à ce que la relation vérifiée par la suite soit linaire et pas affine (c'est à dire sans constante).
Pour la 2),b) c'est O.K., mais je ne comprend pas pourquoi tu met des "n+1" : de toute façon la relation qu'on te demande (évidente vu que c'est la somme des 3 proba.), c'est et elle est bien sûr valable pour tout donc à part compliquer l'écriture, je vois pas l'intérêt de l'écrire avec autre chose que .
Et pour la 2),c), vu que tu peut écrire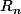 en fonction de et 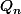, ça te permet d'avoir des formules ne contenant plus de 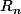et c'est ça qu'on te demande de faire.