l'espace affine euclidienest raporte a un repere orthonormal directe(o,i,j,k).
soit D la droite passant par A(2,1,0)et dirigee par le vecteur u(1,-1,2).
soit D' la droite passant par B(3,3,-1)et dirigee par le vecteur v(2,1,1).
MONTRER QUE D ET D' SONT COPLANAIRES ET FORMER UNE EQUATION CARTESIENNE DU PLAN QUI LES CONTIENT.
Géometrie dans l'espace (1)
10 messages
- Page 1 sur 1
bonjour,
d et d' sont coplanaires si et seulement si elles sont parallèles ou ont (au moins) un point d'intersection.
leurs vecteurs directeurs sont linéairement indépendants. Ces deux droites
affines ne sont pas parallèles. Quant à leur point d'intersection,
il est donné par les systèmes d'inconnues et
et 



qui a pour solution: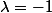 et
et 
conclusion: les droites d et d' sont coplanaires car sécantes en un point.
d et d' sont coplanaires si et seulement si elles sont parallèles ou ont (au moins) un point d'intersection.
leurs vecteurs directeurs sont linéairement indépendants. Ces deux droites
affines ne sont pas parallèles. Quant à leur point d'intersection,
il est donné par les systèmes d'inconnues
qui a pour solution:
conclusion: les droites d et d' sont coplanaires car sécantes en un point.
Le point C d'intersection de d et d' a pour coordonnées:
C(1,2,-2)
l'équation paramétrique du plan passant par C et contenant d et d' est:
 (notation due au mathématicien Grassmann)
(notation due au mathématicien Grassmann)
où dirige la droite affine d et
dirige la droite affine d et  dirige la droite affine d'.
dirige la droite affine d'.
l'équation paramétrique du plan contenant d et d' est donc:



les deux premières équations permettent de calculer et
et  en fonction de x et y. En reportant les valeurs de
en fonction de x et y. En reportant les valeurs de  et
et  dans la troisiéme égalité, on obtient une équation cartésienne du plan.
dans la troisiéme égalité, on obtient une équation cartésienne du plan.
C(1,2,-2)
l'équation paramétrique du plan passant par C et contenant d et d' est:
où
l'équation paramétrique du plan contenant d et d' est donc:
les deux premières équations permettent de calculer
je te résume la discussion:
on commence par regarder les droites vectorielles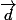 et
et 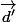
1) si elles ont des vecteurs directeurs proportionnels, alors:

dans ce cas, d et d' sont confondues si elles ont un point d'intersection sinon elles sont parallèles.
2) si leurs vecteurs ne sont pas proportionnels,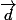 et
et 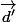 engendrent un plan vectoriel
engendrent un plan vectoriel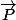 .
.
dans ce cas, si d et d' ont un point d'intersection , alors d et d' sont coplanaires
et le plan qui les contient a pour direction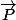
sinon d et d' ne sont pas coplanaires.
on commence par regarder les droites vectorielles
1) si elles ont des vecteurs directeurs proportionnels, alors:
dans ce cas, d et d' sont confondues si elles ont un point d'intersection sinon elles sont parallèles.
2) si leurs vecteurs ne sont pas proportionnels,
dans ce cas, si d et d' ont un point d'intersection , alors d et d' sont coplanaires
et le plan qui les contient a pour direction
sinon d et d' ne sont pas coplanaires.
Dans le message de 11h45, tu résoud le système d'inconnues  et
et 
(2 inconnues,trois équations) et tu calcule la valeur correspondante de x,y,z.
ça donne les coordonnées de C. Pour l'équation cartésienne du plan P
il faut la déterminer connaissant le point C et deux vecteurs de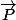
 et
et  qui sont les directions respectives de (d) et (d').
qui sont les directions respectives de (d) et (d').
(2 inconnues,trois équations) et tu calcule la valeur correspondante de x,y,z.
ça donne les coordonnées de C. Pour l'équation cartésienne du plan P
il faut la déterminer connaissant le point C et deux vecteurs de
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
