Résolution d'une équation

[ludovic44]

Bonjour, je ne sais pas si cette question à sa place dans le forum supérieur mais je sèche à la résolution de l'équation:



D'après le Gourdon analyse page 194, un "calcul simple" permet de déterminer les trois solutions.
Merci pour votre aide.
Ludovic

[lyceen95]

Première étape, se ramener à notre zone de confort : les polynômes.
Donc je fais un changement de variable, pour supprimer cette racine carrée : je cherche qui vérifie

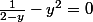
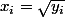
Quand j'aurais trouvé les racines de cette équation, les racines de l'équation originales seront données par avec des contrôles de routines sur le signe des

Et comme je veux travailler avec des polynômes, je multiplie par (2-y) (toujours avec les précautions d'usage), et j'arrive à l'équation polynomiale :

Nous, on sait bien traiter les équations de degré 2, or celle ci est de degré 3.
Et on nous dit qu'il y a 3 racines, et qu'un calcul simple permet de les trouver.
Dans ce cas, ça veut dire qu'il y a une racine facile à trouver.
On regarde si par hasard y=0 ou y=1 ou y=-1 ne seraient pas des racines de cette équation.
On trouve une racine 'évidente' ; on peut donc factoriser , et on se ramène à une équation du 2nd degré.
Et on déroule la machine.

[caillou1]

Bonjour,
J'ai ravalé ma réponse suite à celle de lyceen95
Une précision :

un "calcul simple" permet de déterminer les trois solutions.

A priori il n'y en a que deux.

[Ben314]

Salut,
Pour ce type d'équation, une autre méthode (en général moins bonne, mais pas toujours), c'est d'écrire l'équation sous la forme puis d'élever au carré (en prenant garde à bien préciser que ce qu'il y a à droite du = doit être positif) :