Régression parabolique non triviale

[sylvain231]

une solution bête et méchante est de faire les deux méthodes, de calculer la somme des écarts et de prendre celle qui a cette somme la plus petite possible mais rien ne garantit que ça marche dans d'autres cas pas encore testés

[sylvain231]

j'ai une autre idée mais n'arrive pas à l'implémenter :
parcourir tous les a selon une échelle logarithmique
parcourir tous les theta
calculer les écarts avec la parabole théorique des points de départ avec les points de la parabole et en faire la somme
prendre le a et le theta correspondant au minimum de cette somme

c'est l'écart avec la parabole que je n'arrive pas à calculer
c'est une solution brute force mais elle a l'avantage de marcher du moins je pense

[leon1789]

calculer les écarts avec la parabole théorique des points de départ avec les points de la parabole et en faire la somme

Oui, cela fonctionnerait, mais ce n'est pas simple, même sans paramètre formel.
Arrives-tu à trouver une fonction qui donne la distance entre un point quelconque (u, v) et la parabole y = x^2 ?

superieur/regression-parabolique-non-triviale-t278846-40.html#p1548740

[sylvain231]

non désolé je suis nul en maths mais rechercher la distance d'un point avec une parabole tournée et translatée de paramètres theta et a résoudrait aussitôt notre problème à condition que le calcul ne soit pas trop coûteux en temps

[sylvain231]

j'ai trouvé ça : https://www.physicsforums.com/threads/l ... 20%2Dy%2F4. je n'y comprend rien mais si ça peut t'aider

[sylvain231]

j'ai posé la question à chatGPT voici sa réponse dis-moi ce que tu en penses :

quelle est la distance la plus courte entre un point et une parabole d'équation 0 = a * pow(theta * (x-sommet.x) + sin(theta) * (y-sommet.y), 2)- sin(theta) * (x - sommet.x) - cos(theta) * (y - sommet.y)
ChatGPT
L'équation que vous avez donnée représente une parabole définie par une équation quadratique. Cependant, il manque des informations importantes pour calculer la distance la plus courte entre un point et cette parabole. Plus précisément, il manque les valeurs des variables a, sommet.x, sommet.y et theta.

Pour déterminer la distance la plus courte entre un point et une parabole, vous devez connaître les coordonnées du point et les paramètres qui définissent la parabole. Avec ces informations, vous pouvez utiliser une méthode appelée "distance point-parabole" pour calculer la distance souhaitée.

Si vous fournissez les valeurs appropriées pour les paramètres de la parabole et les coordonnées du point, je serai en mesure de vous aider à calculer la distance la plus courte.





User
ces valeurs sont données je veux l'équation de la distance en fonction de ces paramètres et du x et du y du point dont on cherche la distance avec la parabole
ChatGPT
D'accord, maintenant que nous avons les valeurs des paramètres a, sommet.x, sommet.y et theta, nous pouvons calculer l'équation de la distance entre un point et la parabole.

La distance entre un point (x, y) et une parabole peut être déterminée en calculant la distance perpendiculaire entre le point et la courbe de la parabole. La formule générale pour la distance entre un point et une courbe est donnée par :

Distance = |ax + by + c| / √(a^2 + b^2)

Dans notre cas, l'équation de la parabole est donnée par :

0 = a * (θ * (x - sommet.x) + sin(θ) * (y - sommet.y))^2 - sin(θ) * (x - sommet.x) - cos(θ) * (y - sommet.y)

En comparant cette équation à la forme générale ax + by + c = 0, nous pouvons déterminer les valeurs de a, b et c :

a = a * (θ^2 + sin^2(θ))
b = -2 * a * θ * sin(θ)
c = a * (sin^2(θ) * (sommet.x^2 + sommet.y^2) - sommet.x) + sommet.y * cos(θ)

Maintenant, nous pouvons substituer ces valeurs dans la formule de distance et obtenir l'équation finale :

Distance = |a * (θ * (x - sommet.x) + sin(θ) * (y - sommet.y))^2 - sin(θ) * (x - sommet.x) - cos(θ) * (y - sommet.y)| / √(a^2 + b^2)

Veuillez noter que cette équation donne la distance signée. Si vous voulez la distance absolue, vous pouvez prendre la valeur absolue de l'expression à l'intérieur de la valeur absolue.

J'espère que cela répond à votre question ! Si vous avez d'autres préoccupations, n'hésitez pas à les poser.

[sylvain231]

si ça peut faire avancer le schmilblick

[leon1789]

laisse tomber chatGPT.

La distance entre un point (x, y) et une parabole peut être déterminée en calculant la distance perpendiculaire entre le point et la courbe de la parabole. La formule générale pour la distance entre un point et une courbe est donnée par :

Distance = |ax + by + c| / √(a^2 + b^2)

c'est faux : confusion droite / courbe

Dans notre cas, l'équation de la parabole est donnée par :

0 = a * (θ * (x - sommet.x) + sin(θ) * (y - sommet.y))^2 - sin(θ) * (x - sommet.x) - cos(θ) * (y - sommet.y)

c'est faux ; oublie du cosinus

Etc.

[leon1789]

calculer les écarts avec la parabole théorique des points de départ avec les points de la parabole et en faire la somme
prendre le a et le theta correspondant au minimum de cette somme

Un majorant pas trop mauvais de la distance entre un point et la parabole serait surement suffisant.
theta est compris entre 0 et Pi. Mais la valeur de a n'est pas bornée : il faudra considérer a entre -1 et 1 , et par ailleurs 1/a compris entre -1 et 1.

Mais bon, il faut déjà trouver majorant pas trop mauvais de la distance entre un point et la parabole.

[leon1789]

J'ai bien un truc qui fonctionne sur tes deux exemples. C'est lié au calcul de distance justement. Mais il faut recherche deux à la fois t entre 0 et Pi, et la variable a dans ... les réels...

Je suppose le sommet en (0,0) comme d'habitude.
Tes points sont les ( x[i] , y[i] )

Pour i = 1...n , on calcule
R[i] = a * ( X[i]*cos(t) - Y[i]*sin(t) )

On calcule ensuite la somme S pour i=1...n de
( R[i]^2 * sin(t)/a + R[i] * cos(t)/a - X[i] )^2 + ( R[i]^2 * cos(t) / a - R[i] * sin(t) / a - Y[i] )^2

Il faut trouver t et a pour minimise la somme S.

[leon1789]

Pour ton exemple serré, on trouve
t := 0.858,
a := -2.39
pour un S minimum de 28022

ce qui donne l'équation
0 = 0.0471*x^2 - 13.9*x + 0.109*x*y - 1000 + 16*y - 0.0629*y^2


Et pour ton exemple plat, on trouve
t := 0.524,
a:= 0.955 / 10^3,
pour un S minimum de 1762

ce qui donne l'équation
0 = 0.00199*x^2 - 1.494*x - 0.0023*x*y + 1000 - 2.342*y+ 0.000663*y^2


Les deux graphes sont comme les meilleurs graphes précédents.

[sylvain231]

OK merci je le code, j'étais en voiture tout à l'heure

[Ben314]

Je sais pas si ça correspond à un des trucs que vous avez déjà essayé, mais vu que de tester y=ax^2, ça déconne lorsque le "bon" a est trop petit, on pourrait chercher la parabole sous la forme ax^2-by=0 sous la contrainte a^2+b^2=1 (*)
Pour un angle donné, on cherche donc et tels que l'espérance soit minimale sous la contrainte 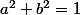ce qui se fait bien y compris sous forme formelle vu que le truc à minimiser est une forme quadratique.

(*) Ce qui en fait signifie que, comme distance d'un point (x,y) à la parabole y=ax^2, on ne va pas prendre |y-ax^2| mais |y-ax^2| / racine(1+a^2) qui, bien évidement donnera un "bonus" aux paraboles avec un très grand a ce qui risque d'éviter que le logiciel approxime avec une parabole tournée de 90 degrés et un a quasi nul.

[sylvain231]

je l'ai codé mais ça ne marche pas pour moi ?!
je te donne mon code pour que tu le vérifie
ah chatGPT est vraiment nul ! mais dans un sens c'est rassurant il ne va pas encore remplacer l'homme

Code: Tout sélectionner

void Parabole::fit(std::vector<cv::Point2d> points, cv::Point2d sommet) {
    this->sommet = sommet;
    int n = points.size();
    cout << "sommet = " << sommet << endl;
    points = translatePoint2ds(points, sommet);
    double minimum = std::numeric_limits<double>::infinity();
    for (int s = -1; s <=1; s += 2) {
        for (double logA = -5; logA <= 5; logA += 0.1) {
            //cout << "logA=" << logA << endl;
            a = s*exp(logA);
            cout << "a=" << a << endl;
            for (double theta = 0; theta <= CV_PI; theta += CV_PI / 1000) {

                double cos_ = cos(theta);
                double sin_ = sin(theta);
                vector<double> R;
                for (int i = 0; i < n; i++) {
                    R.push_back(a * (points[i].x * cos_ + points[i].y * sin_));
                }
                double S = 0;
                for (int i = 0; i < n; i++) {
                    S += pow(pow(R[i], 2) * sin_ / a + R[i] * cos_ / a - points[i].x, 2) + pow(pow(R[i], 2) * cos_ / a - R[i] * sin_ / a - points[i].y, 2);
                }
                if (S < minimum) {
                    minimum = S;
                    this->a = a;
                    this->theta_radians = theta;
                }
            }
        }
    }
    this->theta = 180 * theta_radians / CV_PI;
}


[sylvain231]

allé on y est presque comme ça marche pour toi ça doit être une broutille qui reste pour moi !

[sylvain231]

Ben pourrais-tu détailler l'algo que j'essaie ?

[leon1789]

Ben,
je ne sais pas si cela correspond. Je fais tellement de tests, j'en ai plein la tête.

Sylvain,
La recherche des deux variables t et a n'est pas évidente, je reviens vers toi quand j'aurai avancé.
On va essayer de la faire en deux temps : t entre 0 et Pi, puis le réel a

[sylvain231]

ok merci Léon concentre-toi sur ta méthode, on testera la méthode de Ben que si ça ne marche pas

[leon1789]

Mince, je me suis trompé sur ton exemple serré :
le minimum est ailleurs,
t := 2.39389158
a := -0.001187384179
donne un minimum de 3460 (au lieu de 28022 trouvé avant)
et le graphe n'est pas bon, comme avant.
Désolé.

[sylvain231]

donc encore un coup d'épée dans l'eau, que fait-on tu peux le corriger ou on part sur la méthode de Ben ?