Quand utiliser une analyse synthèse.

[edmath]

Bonjour à tous je me permet d'écrire ce message parce que je suis rentré en prépa MPSI cette année et j'ai découvert le raisonnement par analyse synthèse que je comprends a peut près bien. Mais j'ai un problème c'est que je ne sais jamais quand l'utiliser. Savez vous donc s'il y a une technique pour savoir quand devenons l'utiliser.

Merci d'avance

[mathelot]

...

[GaBuZoMeu]

Bonjour,
La réponse de mathelot pèche en plusieurs points. Déjà à la fin, la façon de trouver un maximum local ne va pas : si et , serait un maximum local de ???
Le raisonnement pas analyse synthèse s'applique typiquement quand on veut démmontrer un énoncé du genre .
Dans la phase analyse, on suppose l'existence d'un tel et on liste les propriétés découlant de pour essayer de trouver une condition nécessaire sur permettant de le caractériser en fonction de .
Dans la phase synthèse, on démontre que le ainsi caractérisé vérifie bien .
Exemple classique et facile : pour toute matrice carrée , il existe un unique couple de matrices avec symétrique et antisymétrique tel que .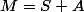
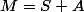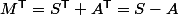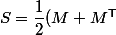Analyse : si un tel couple vérifiant existe, alors , d'où et .
Synthèse : les et donnés par les formules ci-dessus font bien le job. Ils sont respectivement symétrique et antisymétrique, et leur somme est .

[edmath]

Ok je pense comprendre un peu mieux, merci de l'explication

[manlaso]

J'ai rencontré un problème similaire. Installébackrooms, Merci.