Bonjour, Pouvez-vous m'aider s'il vous plaît ?
Enoncé :
Soit KBr -> K + 1/2Br2 la réaction de décomposition du bromure de potassium et la vitesse de reaction : d[KBr ]/dt = k [KBr ]^2(t). On a k = 1,02 L/mol/s et à t = 0s , [KBr](0) = 0,052 mol/L
On considère l’équation différentielle y’(x)+ky²(x) = 0 avec y une fonction non nulle et qui est dérivable sur [0;+infini[
1) Montrer que cette équation différentielle donne l’intégrale suivante : intégrale [0;t] y’(x)/y²(x) dx +kt=0
Trouver l'expression de y(t) en fonction de t, k et la condition initiale y(0)
- J'ai trouvé : y'+ky²=0
y'(x)=-ky²(x)
y'(x)/y²(x)=-k
-1/y(x)=-kt+C
y=1/(kt-C)
Je ne sais pas comment continuer ..
2) Donner l'expression de [KBr](t) en fonction du temps t.
3) Etudier les variation de la fonction [KBr] et tracer la courbe
Equation différentielle et cinétique
12 messages
- Page 1 sur 1
Re: Equation différentielle et cinétique
Bonjour,
y(0) n'est pas dans votre résultat donc vous devriez vous douter que vous avez une erreur.
vous avez :
}{y^2(x)} dx + kt=0) (1)
(1)
calculez :
}{y^2(x)} dx)
et remplacez dans (1)
y(0) n'est pas dans votre résultat donc vous devriez vous douter que vous avez une erreur.
vous avez :
calculez :
et remplacez dans (1)
Re: Equation différentielle et cinétique
Salut,
Ben c'est tout bon.
Et la "condition initiale" qui te dit que, lorsque , on a
, on a \!=\!y_o) (qui est considéré comme connu) te permet de trouver la valeur de la constante
(qui est considéré comme connu) te permet de trouver la valeur de la constante  (qui va bien sûr dépendre de
(qui va bien sûr dépendre de  et de
et de 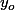 )
)
EDIT (vu que j'ai tapé en même temps que phyelec) : J'ai beau relire dans tout les sens, je vois pas où est-ce que phyelec voit une "erreur" dans ta prose.
Ben c'est tout bon.
Et la "condition initiale" qui te dit que, lorsque
EDIT (vu que j'ai tapé en même temps que phyelec) : J'ai beau relire dans tout les sens, je vois pas où est-ce que phyelec voit une "erreur" dans ta prose.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation différentielle et cinétique
et bien, j'ai réagi sur la consigne c'est tout. Je n'ai pas creusé plus. mea culpa.
Re: Equation différentielle et cinétique
Ben... d'un autre coté, moi j'ai relu 3 fois la réponse de Christophe13, mais j'ai pas lu la consigne . . .
Et effectivement, la méthode employé ne colle pas à 100% avec la consigne qui demande de passer par une intégrale.
Et effectivement, la méthode employé ne colle pas à 100% avec la consigne qui demande de passer par une intégrale.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation différentielle et cinétique
Bonjour, en primitivant je trouve que intégrale [0;t] y’(x)/y²(x) dx = [-1/y(x)][0;t] et je trouve -1/y(t)-(-1/y(0))
Après je ne sais pas comment l'introduire dans l'intégrale comme vous le demandiez
Après je ne sais pas comment l'introduire dans l'intégrale comme vous le demandiez
Re: Equation différentielle et cinétique
Vu que }{y^2(x)}=-k) , c'est que
, c'est que }{y^2(x)}\,dt=-\int_0^t k\,dt=\cdots)
Modifié en dernier par Ben314 le 07 Juin 2023, 23:24, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation différentielle et cinétique
Merci beaucoup, j'ai bien trouvé qu'une primitive de k est kt est je tombe sur l'équation demandée. Finalement, pour exprimer y(t) j'utilise bien [0;t] y’(x)/y²(x) dx +kt = [-1/y(x)][0;t]+kt et ensuite y(t)= -1/y(t)-(-1/y(0))+kt ?
Re: Equation différentielle et cinétique
Ca sort d'où ce truc (en rouge) ?????Christophe13 a écrit:Merci beaucoup, j'ai bien trouvé qu'une primitive de k est kt est je tombe sur l'équation demandée. Finalement, pour exprimer y(t) j'utilise bien [0;t] y’(x)/y²(x) dx +kt = [-1/y(x)][0;t]+kt et ensuite y(t)= -1/y(t)-(-1/y(0))+kt ?
Si au lieu d'écrire (comme dans mon message précédent) que
Et dans ce cas, ce que tu as, c'est bien évidement
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation différentielle et cinétique
pour le truc en rouge je me suis trompé je trouve finalement y(t) = 1/(1/y(0) + kt). Ce résultat est trouvé lorsque je primitive l'intégrale puis j'isole y(t) puisqu'on veut l'expression de y(t). Ce n'est pas ça ?
Re: Equation différentielle et cinétique
Oui, c'est ça.
Et tu pouvait parfaitement obtenir la même chose en procédant comme tu l'a fait dans ton premier message où tu as obtenu :
y(t)=1/(kt-C) où C est une constante.
Tu écrit ensuite que, lorsque t=0, tu as
y(0)=-1/C et donc C=-1/y(0) et y(t)=1/(kt+1/y(0))
Et tu pouvait parfaitement obtenir la même chose en procédant comme tu l'a fait dans ton premier message où tu as obtenu :
y(t)=1/(kt-C) où C est une constante.
Tu écrit ensuite que, lorsque t=0, tu as
y(0)=-1/C et donc C=-1/y(0) et y(t)=1/(kt+1/y(0))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
