Bonjour,
Voici une équation sur internet:
Résoudre x^(x^3)=36
.
.
.
On arrive à: ((x^3))^(x^3)= =6^6, jusque là ça va
Mais on déduit: (x^3)=6
Je ne connais pas une formule du genre a^n = b^m, alors n=m et a=b
Voici le lien:
https://www.youtube.com/watch?v=DMDUT1iZ-XY
Merci d'avance.
Les puissances
7 messages
- Page 1 sur 1
Re: Les puissances
Bonjour
En fait ce n'est pas une déduction c'est juste une condition suffisante, c'est à dire que si
 alors
alors ^{x^3}=6^6)
donc c'est une solution mais on ne sait pas si c'est la seule, pour le démontrer dans la video il fait une étude de la fonction et démontre qu'elle est unique, c'est donc
Attention toutefois dans la video il n'utilise pas de parenthèses alors que l'exponentiation n'est pas associative, à mon sens c'est génant...
En effet^3) n'est pas égal à
n'est pas égal à })
kadaid a écrit:On arrive à: ((x^3))^(x^3)= =6^6, jusque là ça va
Mais on déduit: (x^3)=6
En fait ce n'est pas une déduction c'est juste une condition suffisante, c'est à dire que si
donc c'est une solution mais on ne sait pas si c'est la seule, pour le démontrer dans la video il fait une étude de la fonction et démontre qu'elle est unique, c'est donc
Attention toutefois dans la video il n'utilise pas de parenthèses alors que l'exponentiation n'est pas associative, à mon sens c'est génant...
En effet
Re: Les puissances
Bonjour,
Les règles de priorité pour les puissances ne laissent pas d'ambiguïté : , c'est toujours
, c'est toujours  à la puissance
à la puissance  , et jamais
, et jamais 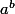 à la puissance
à la puissance  .
.
Les règles de priorité pour les puissances ne laissent pas d'ambiguïté :
Re: Les puissances
Salut,
Perso, j'aurais tendance à considérer que de définir comme étant égal à
comme étant égal à }) c'est plutôt du bon sens vu que la deuxième option, à savoir
c'est plutôt du bon sens vu que la deuxième option, à savoir ^c}) peut s'écrire plus simplement
peut s'écrire plus simplement 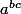 .
.
Sauf qu'ensuite, force est de constater que, surtout à l'heure actuelle, le bon sens, c'est pas le truc le mieux partagé chez l'homo sapiens sapiens . . . (la coté "mouton de Panurge" domine plus que largement...)
Oui, enfin, faut faire gaffe quand même, en particulier si on utilise un langage de programmation ou un tableur => WIKIGaBuZoMeu a écrit:Les règles de priorité pour les puissances ne laissent pas d'ambiguïté :, c'est toujours
à la puissance
, et jamais
à la puissance
.
Perso, j'aurais tendance à considérer que de définir
Sauf qu'ensuite, force est de constater que, surtout à l'heure actuelle, le bon sens, c'est pas le truc le mieux partagé chez l'homo sapiens sapiens . . . (la coté "mouton de Panurge" domine plus que largement...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Les puissances
kadaid a écrit:J'ai fait une faute de frappe
a^x=b implique: (a^x)^(a^x)=b^b
Oui puisque
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
