Bonjour à tous , j'envoi ce message pour savoir si quelqu'un pouvais corrigé cet exercice (exercice 1)svp?
https://zupimages.net/viewer.php?id=23/19/dlho.jpeg
Complexe, racine polynômes
8 messages
- Page 1 sur 1
Re: Complexe, racine polynômes
GaBuZoMeu a écrit:Bonjour,
Propose ta solution !
Bonjour désolé en général je poste ma solution mais je révise pour des exam
voici toutefois des éléments de réponse(j'ai essayé )
https://zupimages.net/viewer.php?id=23/19/t2gz.jpeg
Re: Complexe, racine polynômes
Je n'ai pas compris ce que tu as voulu écrire
En fait quand on te demande de montrer que les conditions sont équivalentes, on te demande de montrer, si on note par exemple (A) et (B) chacune de ces propositions :
(A) P(a) = 0 càd a est racine de P
(B) (X-a) divise P
que (A) implique (B) et (B) implique (A)
Ok, faisons (A) implique (B) :
Soit racine de
racine de  c'est à dire
c'est à dire  = 0)
On a = P(X) - 0 = P(X) - P(a))
 est un polynôme. Appelons
est un polynôme. Appelons  son degré. Il s'écrit
son degré. Il s'écrit  = \sum_{k=0}^d p_k X^k) et donc :
et donc :
 - P(a) = \sum_{k=0}^d p_k X^k - \sum_{k=0}^d p_k a^k = \sum_{k=0}^d p_k (X^k - a^k)) . Si tu connais ta formule de factorisation, tu sais que
. Si tu connais ta formule de factorisation, tu sais que 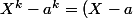 \sum_{j=0}^{k-1} a^{k-1-j}(-1)^jX^j) (ou plus simplement tu sais que
(ou plus simplement tu sais que 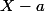 divise
divise  , peu importe comment il s'écrit formellement) et alors :
, peu importe comment il s'écrit formellement) et alors :
 = (X-a) \sum_{k=0}^d p_k \sum_{j=0}^{k-1} a^{k-1-j}(-1)^j X^j) c'est à dire
c'est à dire 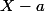 divise
divise 
Faisons (B) implique (A) c'est beaucoup plus simple :
Si) divise
divise  alors
alors  s'écrit
s'écrit  = (X-a)Q(X)) où
où  est un polynôme. En appliquant en
est un polynôme. En appliquant en  il vient que
il vient que  = (a-a)Q(a) = 0) donc
donc  est racine de
est racine de 
En fait quand on te demande de montrer que les conditions sont équivalentes, on te demande de montrer, si on note par exemple (A) et (B) chacune de ces propositions :
(A) P(a) = 0 càd a est racine de P
(B) (X-a) divise P
que (A) implique (B) et (B) implique (A)
Ok, faisons (A) implique (B) :
Soit
On a
Faisons (B) implique (A) c'est beaucoup plus simple :
Si
Re: Complexe, racine polynômes
Faisons la même chose pour les conditions suivantes :
(A) Pour tout
}(a) = 0) pour tout
pour tout 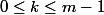 et
et } \ne 0)
(B)^m) divise
divise  mais
mais ^{m+1}) ne divise pas
ne divise pas 
Faisons (B) implique (A) :
Soit^m) divisant
divisant  . Alors
. Alors  s'écrit
s'écrit  = (X-a)^mQ(X)) où
où  est un polynôme non divisible par
est un polynôme non divisible par 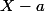 . Dérive une fois le polynôme et tu auras
. Dérive une fois le polynôme et tu auras  = m(X-a)^{m-1}Q(X) + (X-a)^m Q'(X)) . En
. En  cela vaut
cela vaut  donc
donc  = 0) .
.
En réalité, si tu dérives fois ce polynôme
fois ce polynôme  tu auras dans chacun de tes termes un facteur
tu auras dans chacun de tes termes un facteur 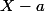 , ce qui annule
, ce qui annule }(a)) , et ce jusqu'à ce que
, et ce jusqu'à ce que  . Si maintenant
. Si maintenant  c'est à dire si tu dérives
c'est à dire si tu dérives  fois ce polynôme, tu vas te retrouver avec uniquement des termes de la forme
fois ce polynôme, tu vas te retrouver avec uniquement des termes de la forme ^{bidule \ge 1}) sauf un seul ! (fais le calcul), le terme qui était de la forme
sauf un seul ! (fais le calcul), le terme qui était de la forme ^1 Q(X)) dans
dans }(X)) .
.
Il se trouve que (là encore, faire le calcul) vaut
(là encore, faire le calcul) vaut 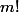 donc
donc }(a) = m!Q(a)) et comme
et comme  \ne 0) car
car ) ne divise pas
ne divise pas  par hypothèse,
par hypothèse, }(a) \ne 0)
Là j'ai dégrossi pour donner l'idée, en toute logique il faut démontrer formellement avec une récurrence
(A) Pour tout
(B)
Faisons (B) implique (A) :
Soit
En réalité, si tu dérives
Il se trouve que
Là j'ai dégrossi pour donner l'idée, en toute logique il faut démontrer formellement avec une récurrence
Re: Complexe, racine polynômes
On montre (B) implique (A) par récurrence sur 
INITIALISATION :
Quand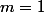 : on suppose que
: on suppose que 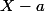 divise
divise  mais que
mais que ^2) ne divise pas
ne divise pas  donc
donc  s'écrit nécessairement
s'écrit nécessairement  = (X-a)Q(X)) avec
avec 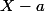 qui ne divise pas
qui ne divise pas  .
.
Alors = Q(X) + (X-a)Q'(X)) donc
donc  = Q(a) \ne 0) car
car  n'est pas racine de
n'est pas racine de
donc}(a) = P'(a) \ne 0) mais
mais }(a) = P(a) = 0) (la dérivée
(la dérivée 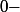 ième d'une fonction c'est... la fonction elle-même) car
ième d'une fonction c'est... la fonction elle-même) car  racine de
racine de 
HÉRÉDITÉ :
On suppose que l'implication est vraie pour un certain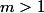 . Montrons qu'alors l'implication reste vraie pour
. Montrons qu'alors l'implication reste vraie pour 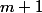 c'est à dire montrons que si
c'est à dire montrons que si ^{m+1}) divise
divise  mais
mais ^{m+2}) ne divise pas
ne divise pas  alors
alors } = 0) pour tout
pour tout 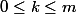 et
et }(a) \ne 0)
Soit donc^{m+1}) qui divise
qui divise  mais
mais ^{m+2}) qui ne divise pas
qui ne divise pas  . Alors
. Alors  s'écrit nécessairement
s'écrit nécessairement  = (X-a)^{m+1}Q(X)) où
où  est un polynôme qui n'est pas divisible par
est un polynôme qui n'est pas divisible par )
Alors = (m+1)(X-a)^mQ(X) + (X-a)^{m+1}Q'(X))
^m) divise
divise  mais pas
mais pas ^{m+1}) . Par hypothèse de récurrence,
. Par hypothèse de récurrence, }(a),...,P'^{(m-1)}(a) = P^{(2)}(a)...P^{(m)}(a) = 0) et
et } = P^{(m+2)} \ne 0) . De plus
. De plus  = 0) . Le résultat est démontré au rang
. Le résultat est démontré au rang 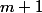
INITIALISATION :
Quand
Alors
donc
HÉRÉDITÉ :
On suppose que l'implication est vraie pour un certain
Soit donc
Alors
Re: Complexe, racine polynômes
Salut,
Perso, j'aurais franchement pas procédé comme ça...
Un polynôme, c'est un truc de la forme=a_0+a_1X+a_2X^2+...+a_dX^d) et, dès qu'on voit la notion de dérivation formelle des polynômes, c'est pas idiot de constater que
et, dès qu'on voit la notion de dérivation formelle des polynômes, c'est pas idiot de constater que =a_0) ;
; =a_1) ;
; =2a_2) ; ;
; ; =6a_3) ; ... ;
; ... ; }(0)=d!a_d) et d'en déduire que, si
et d'en déduire que, si  est de caractéristique nulle, pour tout
est de caractéristique nulle, pour tout  on a :
on a :
=P(a)+P'(a)(X-a)+\frac{1}{2}P''(a)(X-a)^2+\frac{1}{6}P'''(a)(X-a)^3+...+\frac{1}{d!}P^{(d)}(a)(X-a)^d)
qui se démontre simplement en appliquant les relations précédentes (qui, elles, sont triviales) au polynôme=P(a+X)) et qui, comme par hasard, ressemble étrangement à la formule des développement limités sauf que là, c'est une vrai égalité.
et qui, comme par hasard, ressemble étrangement à la formule des développement limités sauf que là, c'est une vrai égalité.
Et cette formule te dit par exemple que le reste de la division euclidienne de) par
par ^3) , ben c'est
, ben c'est +P'(a)(X-a)+\frac{1}{2}P''(a)(X-a)^2) donc c'est zéro ssi
donc c'est zéro ssi =P'(A)=P''(a)=0) .
.
Perso, j'aurais franchement pas procédé comme ça...
Un polynôme, c'est un truc de la forme
qui se démontre simplement en appliquant les relations précédentes (qui, elles, sont triviales) au polynôme
Et cette formule te dit par exemple que le reste de la division euclidienne de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Complexe, racine polynômes
Bonjour,
Salut Ben314, de retour après une longue absence !
Je trouve que la récurrence est tout à fait adaptée ici.
Il suffit en fait de montrer que=\ldots=P^{(n)}(a)=0) équivaut à
équivaut à ^{n+1}\mid P) , par récurrence sur
, par récurrence sur  .
.
L'initialisation est conséquence immédiate de la division euclidienne par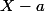 .
.
Supposons le résultat vrai pour .
.
Si est divisible par
est divisible par ^{n+2}) , alors
, alors =0) et comme
et comme ) est divisible par
est divisible par ^{n+1}) on a par hypothèse de récurrence
on a par hypothèse de récurrence =\ldots=P^{(n+1)}(a)=0) .
.
Si=\ldots=P^{(n)}(a)=P^{(n+1)}(a)=0) alors par hypothèse de récurrence il existe un polynôme
alors par hypothèse de récurrence il existe un polynôme  tel que
tel que 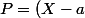^{n+1}Q) et
et ^n((n+1)Q+(X-a)Q')) est aussi divisible par
est aussi divisible par ^{n+1}) . Ceci entraîne que
. Ceci entraîne que  est divisible par
est divisible par 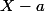 (on utilise ici
(on utilise ici  ).
).
Salut Ben314, de retour après une longue absence !
Je trouve que la récurrence est tout à fait adaptée ici.
Il suffit en fait de montrer que
L'initialisation est conséquence immédiate de la division euclidienne par
Supposons le résultat vrai pour
Si
Si
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
