Portée d’une flèche
9 messages
- Page 1 sur 1
 Portée d’une flèche
Portée d’une flèche
Bonjour , j’aimerais calculer la portée d’une flèche sachant qu’elle monte à 650 m de hauteur max et qu’elle parcourt 559 km en l’air . Pouvez vous m’aider ?
Re: Portée d’une flèche
Je crois à un exercice en physique lol.
Pour calculer la portée, tu dois utiliser le théorème de Pythagore. Selon mon intuition, la réponse sera négative, ce qui ne signifie pas de solution réelle. Cela peut être dû à un manque de données, à une intuition erronée de ma part. Cependant, en physique, tout s'explique, donc je t'encourage à effectuer les calculs nécessaires et de nous tenir au jus.
Bonne soirée!
Pour calculer la portée, tu dois utiliser le théorème de Pythagore. Selon mon intuition, la réponse sera négative, ce qui ne signifie pas de solution réelle. Cela peut être dû à un manque de données, à une intuition erronée de ma part. Cependant, en physique, tout s'explique, donc je t'encourage à effectuer les calculs nécessaires et de nous tenir au jus.
Bonne soirée!
Re: Portée d’une flèche
« Du ciel vient la lumière
Alors prête un arc à Apollon : de là, il comptera 1969,697 mesures vers le zénith. En une 46.241.860ème fraction de jour sidéral, son trait s'abattra. »
Voila le texte de l’énigme, qu’en pensez-vous ?
Alors prête un arc à Apollon : de là, il comptera 1969,697 mesures vers le zénith. En une 46.241.860ème fraction de jour sidéral, son trait s'abattra. »
Voila le texte de l’énigme, qu’en pensez-vous ?
Re: Portée d’une flèche
Mais on manque scrupuleusement d'info..... BON J'essaye :
Du ciel vient la lumièere → ferions-nous réf à une étoile ?
Alors prête un arc à Apollon → mesure d'un angle ? angle entre la supposée étoile et Zénith ?
de là, il comptera 1969,697 mesures vers le zénith → mesure d'angle très certainement, mais degrés ou radians ?
En une 46.241.860ème fraction de jour sidéral, son trait s'abattra → indication de temps
Hmm
Du ciel vient la lumièere → ferions-nous réf à une étoile ?
Alors prête un arc à Apollon → mesure d'un angle ? angle entre la supposée étoile et Zénith ?
de là, il comptera 1969,697 mesures vers le zénith → mesure d'angle très certainement, mais degrés ou radians ?
En une 46.241.860ème fraction de jour sidéral, son trait s'abattra → indication de temps
Hmm
Re: Portée d’une flèche
Hé, YES, j'ai trouvé la source :
http://piblo29.free.fr/wiki_chouette/in ... Enigme_420
http://piblo29.free.fr/wiki_chouette/in ... Enigme_420
Re: Portée d’une flèche
Oui si tu ne connais pas la chouette d’or , c’est totalement passionnant !!! Il est souvent « admis » que 650 m corresponds à l’altitude du point d’arriver mais je voulais essayer de voir le problème autrement …
Re: Portée d’une flèche
Hello,
On peut se placer dans un repère) et supposer que la flèche est tirée depuis l'origine. On note
et supposer que la flèche est tirée depuis l'origine. On note  la distance à l'origine où la flèche atterit. C'est notre inconnue !
la distance à l'origine où la flèche atterit. C'est notre inconnue !
Sa trajectoire est donc une parabole de la forme = -ax\cdot(x-d)) avec
avec  une autre inconnue. On peut commencer par traduire le fait que la flèche monte jusqu'à
une autre inconnue. On peut commencer par traduire le fait que la flèche monte jusqu'à 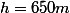 . C'est le point culmunant atteint donc lorsque
. C'est le point culmunant atteint donc lorsque =0) , en
, en  Ca nous donne
Ca nous donne  et on peut donc exprimer
et on peut donc exprimer  en fonction de
en fonction de  . Pour déterminer
. Pour déterminer  on peut alors traduire le fait que la distance parcourue est
on peut alors traduire le fait que la distance parcourue est  km mais c'est plus compliqué. Il s'agit de la longueur de l'arc de parabole entre ses deux racines ;
km mais c'est plus compliqué. Il s'agit de la longueur de l'arc de parabole entre ses deux racines ;  et
et  . Cette longueur est donnée par
. Cette longueur est donnée par 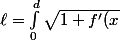^2}dx) . Sauf que cette intégrale à l'air assez pénible à calculer. Il y a un calcul de primitive pour l'arc de la parabole
. Sauf que cette intégrale à l'air assez pénible à calculer. Il y a un calcul de primitive pour l'arc de la parabole  (donc le calcul de
(donc le calcul de  ) dans le lien suivant :
) dans le lien suivant :
http://serge.mehl.free.fr/anx/long_arc_parabole.html
Peut-être faudrait-il essayer avec un changement de variable adéquat (ou une méthode moins calculatoire) ! À la fin on devrait avoir une nouvelle équation en fonction de et
et  . Grâce à
. Grâce à  , ça donnera une équation en
, ça donnera une équation en  seulement. À voir si on pourra la résoudre facilement
seulement. À voir si on pourra la résoudre facilement  .
.
En espérant avoir pu t'aider !
On peut se placer dans un repère
Sa trajectoire est donc une parabole de la forme
http://serge.mehl.free.fr/anx/long_arc_parabole.html
Peut-être faudrait-il essayer avec un changement de variable adéquat (ou une méthode moins calculatoire) ! À la fin on devrait avoir une nouvelle équation en fonction de
En espérant avoir pu t'aider !
Re: Portée d’une flèche
Il est bien connu que la portée maximale d'une flèche s'obtient en la tirant à 45° (on fait abstraction de la résistance de l'air, du vent etc.).
Si elle a parcouru en l'air une trajectoire parabolique de longueur avec apogée à la hauteur
avec apogée à la hauteur  au dessus du sol, la distance du point de départ au point de chute ne donnera la portée maximale que si l'angle de la vitesse au départ sur l'horizontale est de 45°.
au dessus du sol, la distance du point de départ au point de chute ne donnera la portée maximale que si l'angle de la vitesse au départ sur l'horizontale est de 45°.
Si elle a parcouru en l'air une trajectoire parabolique de longueur
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
