Bonjour chers mathématiciens.
J'espère que vous pourrez m'aider.
Tout d'abord, voici la situation sur laquelle je travaille : "Un joueur lance une pièce équilibrée et se donne un point pour chaque fois que la pièce tombe sur face, ainsi que deux points pour chaque fois que la pièce tombe sur pile."
Il me faut d'abord trouver une séquence définie récursivement qui donne la probabilité d'atterrir sur n points (sachant que n points peuvent être atteints en obtenant pile après avoir eu n−1 points, ou pile après avoir eu n−2 points).
J'ai trouvé que P(n)=1/2*P(n-1) + 1/2*P(n-2) avec n>=2.
Maintenant, je dois montrer par récurrence que P(n)=1/3[2+(-1/2)^n].
Pour l'initialisation c'est bien, c'est vrai pour n=0 ou n=1. Mais j'ai du mal avec l'approche suite à mon hypothèse que c'est aussi vrai pour n+1.
J'ai commencé avec P(k+1)=1/2P(k) + 1/2P(k-1)
qui peut être réécrit comme :
P(k+1)=1/2(1/3[2+(-1/2)^k]) + 1/2(1/3[2+(-1/2)^k-1])
Et:
P(k+1)=1/6(4 + (-1/2)^k + (-1/2)^k-1)
Mais maintenant je ne sais plus quoi en faire...
En espérant que vous pourrez m'aider !
Merci beaucoup!
Preuve par récurrence sur la probabilité d'avoir n points
6 messages
- Page 1 sur 1
Preuve par récurrence sur la probabilité d'avoir n points
Modifié en dernier par fonuni le 27 Avr 2023, 17:56, modifié 1 fois.
Re: Preuve par récurrence sur la probabilité d'avoir n point
Bonjour,
Relis-toi et corrige.
"Un joueur lance une pièce équilibrée et se donne un point pour chaque fois que la pièce tombe sur pile, ainsi que deux points pour chaque fois que la pièce tombe sur pile."
Relis-toi et corrige.
Re: Preuve par récurrence sur la probabilité d'avoir n point
Bonjour
En efet l'énoncé est loin d'être clair...
Toutefois en admettant que ce soit juste
On peut factoriser^k + (\dfrac{-1}{2})^{k-1})
sous la forme^{k-1}(\dfrac{-1}{2}+1))
En efet l'énoncé est loin d'être clair...
Toutefois en admettant que ce soit juste
On peut factoriser
sous la forme
Re: Preuve par récurrence sur la probabilité d'avoir n point
Bonjour GaBuZoMeu et catamat, en effet, désolé pour cette erreur de frappe, j'ai corrigé. Donc je voulais plutôt dire 1 point pour face et 2 points pour pile. Finalement, j'ai réussi à factoriser (-1/2)^k + (-1/2)^k-1 sous la forme (-1/2)^k+1 *2.
Merci quand même!
Merci quand même!
Re: Preuve par récurrence sur la probabilité d'avoir n point
pour confronter tes formules avec la réalité:
saisir N
T prend la valeur 0
pour I de 1 à 1000
S prend la valeur 0
tant que S<N faire
R prend la valeur aléa{0,1}
S prend la valeur
fin tant que
si S=N
T prend la valeur T+1
fin si
I suivant
afficher T/1000
saisir N
T prend la valeur 0
pour I de 1 à 1000
S prend la valeur 0
tant que S<N faire
R prend la valeur aléa{0,1}
S prend la valeur
fin tant que
si S=N
T prend la valeur T+1
fin si
I suivant
afficher T/1000
Re: Preuve par récurrence sur la probabilité d'avoir n point
sais tu résoudre les suites qui vérifient 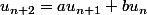 ?
?
Connais tu leur équation caractéristique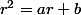 ?
?
Si oui ton exo est immédiat.
Connais tu leur équation caractéristique
Si oui ton exo est immédiat.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
